EM算法详解

极大似然估计
极大似然的本质是找出与样本分布最接近的概率分布模型，它是一种用样本来估计概率模型参数的方法。下面以二项分布和高斯分布为例。

1.二项分布
例如，进行抛硬币实验，十次抛硬币的结果是：$$正正反正正正反反正正$$假设p是每次抛硬币结果为正的概率，则，得到实验结果的概率是，
$$\begin{array}{l} P = pp(1 – p)ppp(1 – p)(1 – p)pp\\ ;;;; = {p^7}{(1 – p)^3} \end{array}$$
而极大似然估计的原理就是让得到实验结果的概率最大，即求得一个参数p使得整个式子最大。

那么对上式求导，得，${P^{'}} = 7 – 10p = 0$，所以求得的p=0.7，即在极大似然估计下求得的正面朝上的概率是0.7。这是一个符合样本分布的结果，因为在10次实验中，有7次是朝上的。

有人说这可能与平常我们认为的不同，对于抛硬币正反的概率不应该是0.5吗？即，每次出现正反的概率都一样才对。那么，这里算出的正面朝上的概率为0.7其实是在极大似然估计下的参数，这完全是基于样本获得的，样本有7次朝上，总共做了10次实验，那么显然，通过样本计算出的正面朝上的概率就是0.7，这就体现了极大似然估计以样本来算参数的原理。

对上述问题进行抽象。在抛硬币的实验中，进行N次独立的实验，n次朝上，N-n次朝下，假设朝上的概率为p，则其似然函数为，
$$f = {p^n}{(1 – p)^{N – n}}$$
一般，似然函数为连乘的形式，不好求导，所以，一般对似然函数取对数，即对数似然函数，
$$\log (f) = \log ({p^n}{(1 – p)^{N – n}}) = n\log (p) + (N – n)\log (1 – p)$$
对上式求导，即，$\frac{{\partial (\log f)}}{{\partial p}} = \frac{n}{p} – \frac{{N – n}}{{1 – p}} = 0$，求得，$p = \frac{n}{N}$。这个结果很显然是符合实验结果分布的。

2.高斯分布
给定一组样本${x_1},{x_2}, \cdots ,{x_n}$，已知它们服从高斯分布$N(u,\sigma )$，试用极大似然估计估计它们的参数$u,\sigma$。

已知高斯分布的概率密度函数为，
$$f(x) = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ – \frac{{{{(x – u)}^2}}}{{2{\sigma ^2}}}}}$$
将样本带入，建立极大似然函数，
$$L(x) = \prod\limits_{i = 1}^n {\frac{1}{{\sqrt {2\pi } \sigma }}} {e^{ – \frac{{{{({x_i} – u)}^2}}}{{2{\sigma ^2}}}}}$$
取对数似然函数，
$$\begin{array}{l} l(x) = \log (L(x)) = \log (\prod\limits_{i = 1}^n {\frac{1}{{\sqrt {2\pi } \sigma }}{e^{ – \frac{{{{(x – u)}^2}}}{{2{\sigma ^2}}}}}} )\\ ;;;;;;;;;;;;;;;;;;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ; = \sum\limits_{i = 1}^n {\log (\frac{1}{{\sqrt {2\pi } \sigma }}{e^{ – \frac{{{{(x – u)}^2}}}{{2{\sigma ^2}}}}})} \\ ;;;;;;;;;;;;;;;;;;;;;;; {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ; = {\sum\limits_{i = 1}^n {\log (2\pi {\sigma ^2})} ^{ – \frac{1}{2}}} + \sum\limits_{i = 1}^n { – \frac{{{{(x – u)}^2}}}{{2{\sigma ^2}}}} \\ ;;;;;;;;;;;;;;;;;;;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ; = – \frac{n}{2}\log (2\pi {\sigma ^2}) – \frac{1}{{2{\sigma ^2}}}\sum\limits_{i = 1}^n {{{(x – u)}^2}} \ \end{array}$$

对 $u,\sigma$求偏导，
$$\frac{{\partial l(x)}}{{\partial u}} = \frac{1}{{{\sigma ^2}}}\sum\limits_{i = 1}^n {({x^i} – u)} = \frac{1}{{{\sigma ^2}}}(\sum\limits_{i = 1}^n {{x^i} – } nu) = 0$$$$\frac{{\partial l(x)}}{{\partial \sigma }} = – \frac{n}{\sigma } + \frac{1}{{{\sigma ^3}}}\sum\limits_{i = 1}^n {{{({x_i} – u)}^2}} = 0$$
求得的结果如下，
$$\begin{array}{l} u = \frac{1}{n}\sum\limits_{i = 1}^n {{x^i}} \\ {\sigma ^2} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({x_i} – u)}^2}} \end{array}$$

上述结论与矩估计是一致的，并且意义很直观：样本的均值即高斯分布的均值，样本的伪方差(不说方差，是因为无偏估计的方差是除以n-1的，而不是这里的n)为高斯分布的方差。

Jensen不等式

• 若f函数为凸函数：

• 基本的Jensen不等式 ：

$$f(\theta x + (1 – \theta )y) \le \theta f(x) + (1 – \theta )f(y)$$
* k维的Jensen不等式 ：
若${\theta _1}, \cdots ,{\theta _k} \ge 0,{\theta _1} + \cdots + {\theta _k} = 1$，则，
$$f({\theta _1}{x_1} + \cdots + {\theta _k}{x_k}) \le {\theta _1}f({x_1}) + \cdots + {\theta _k}f({x_k})$$
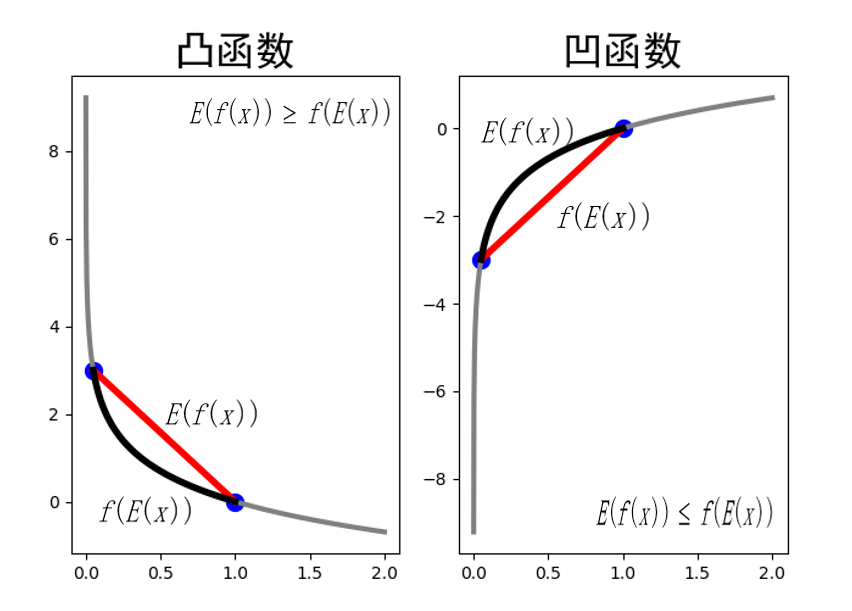
换一个看待的方式，把$\theta$看作随机变量，则上式的含义就是对于凸函数而言，期望的函数小于等于函数值得期望，即，
$$f(E(x)) \le E(f(x))$$

• 若f函数为凹函数： 结论恰好相反，即，

$$f({\theta _1}{x_1} + \cdots + {\theta _k}{x_k}) \ge {\theta _1}f({x_1}) + \cdots + {\theta _k}f({x_k})$$

可用下面这张图来解释，

三硬币例子——隐变量

先看一个抛三硬币例子，假设有A,B,C这3枚硬币，它们正面向上的概率分别是$\pi ,p和q$。进行如下的抛硬币实验：先抛硬币A，根据其结果选出硬币B和硬币C，正面选择硬币A，反面选C；然后抛选出的硬币，出现正面记作1，出现反面记作0；独立重复n次实验，假设n=10，观测结果如下：1，1，0，1，0，0，1，0，1，1。若只知道观测到的硬币结果，而不知道抛硬币的过程，那么，如何来估计这三枚硬币正面朝上的概率。

上例中，一次实验结果是能直接观测到的(即B或C的结果)，这就是观测变量(observable variable)，这里记作随机变量y；而上例中硬币A的结果是观测不到的，这就是隐变量(latent variable)，用随机变量z表示；$\theta = (\pi ,p,q)$是模型参数，即A,B,C这三枚硬币正面朝上的概率。

对上例进行建模，则模型可以写作，
$$\begin{array}{l} P(y|\theta ) = \sum\limits_z {P(y,z|\theta )} = \sum\limits_z {P(z|\theta )P(y|z,\theta )} \ ;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \pi {p^y}{(1 – p)^{1 – y}} + (1 – \pi ){q^y}{(1 – q)^y} \end{array}$$

若将观测数据用$Y = { {Y_1},{Y_2}, \cdots ,{Y_n}}$表示，未观测数据用$Z = { {Z_1},{Z_2}, \cdots ,{Z_n}}$表示，则观测数据的似然函数为，
$$P(Y|\theta ) = \sum\limits_z {P(Z|\theta )} P(Y|Z,\theta )$$
对数似然函数为，
$$l(y) = \log (P(Y|\theta )) = \log (\sum\limits_z {P(Z|\theta )P(Y|Z,\theta )} )$$
因为log函数里有求和，又含有隐变量，所以不好求解导数，对于上述含有隐变量的极大似然估计，可以用EM算法求解。

EM算法推导

那么，EM算法其实就是对于上述含有隐变量的概率模型极大似然估计。

当面对一个含有隐变量的概率模型时，当然，目标还是极大化观测数据Y关于$\theta$的似然函数，即，
$$\begin{array}{l} l(\theta ) = \log P(Y|\theta ) = \log \sum\limits_z {(Y,Z|\theta )} \ ;;;;;;\ = \log (\sum\limits_z {P(Y|Z,\theta )P(Z|\theta )} ) \end{array}$$

既然上式不好直接求解，那么就考虑迭代法求解。假设在第i次迭代后$\theta$的估计值为${\theta ^{(i)}}$。那么，下次就希望新估计的$\theta$值，可以使$l(\theta )$增加，即 $l({\theta ^{(i + 1)}}) > l({\theta ^{(i)}})$。这样一步步迭代下去，就能达到极大值，为此，可以考虑两者之差，

$$\begin{array}{l} l(\theta ) – l({\theta ^{(i)}}) = \log (\sum\limits_z {P(Y|Z,\theta )} P(Z{\rm{|}}\theta )){\rm{ – }}\log P(Y|{\theta ^{(i)}})\\ ;;;;;;;;;;;;;;;;;;;\ = \log (\sum\limits_z {P(Z|Y,{\theta ^{(i)}})\frac{{P(Y|Z,\theta )P(Z{\rm{|}}\theta )}}{{P(Z|Y,{\theta ^{(i)}})}}} ){\rm{ – }}\log P(Y|{\theta ^{(i)}})\\ ;;;;;;;{\kern 1pt} {\kern 1pt} \mathop \ge \limits^{(凹函数的Jensen不等式)} \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log (\frac{{P(Y|Z,\theta )P(Z{\rm{|}}\theta )}}{{P(Z|Y,{\theta ^{(i)}})}})} {\rm{ – }}\log P(Y|{\theta ^{(i)}})\ ;;;;;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \end{array}$$

令，
$$B(\theta ,{\theta ^{(i)}}) = l({\theta ^{(i)}}) + \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log (\frac{{P(Y|Z,\theta )P(Z{\rm{|}}\theta )}}{{P(Z|Y,{\theta ^{(i)}})}})} {\rm{ – }}\log P(Y|{\theta ^{(i)}})$$
则，
$$l(\theta ) \ge B(\theta ,{\theta ^{(i)}})$$
此时，函数$B(\theta ,{\theta ^{(i)}})$是$l(\theta )$的一个下界函数。

则，任何可以使$B(\theta ,{\theta ^{(i)}})$增大的$\theta$，也可以使$l(\theta )$增大，为了使$l(\theta )$有尽可能大的增长，那么在第i+1次迭代中，应选择${\theta ^{(i + 1)}}$使得$B(\theta ,{\theta ^{(i)}})$达到极大，即，

$${\theta ^{(i + 1)}} = \arg \mathop {\max }\limits_\theta B(\theta ,{\theta ^{(i)}})$$
省去对$\theta$的极大化而言是常数的项，有，
$$\begin{array}{l} {\theta ^{(i + 1)}} = \arg \mathop {\max }\limits_\theta l({\theta ^{(i)}}) + \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log (\frac{{P(Y|Z,\theta )P(Z{\rm{|}}\theta )}}{{P(Z|Y,{\theta ^{(i)}})}})} {\rm{ – }}\log P(Y|{\theta ^{(i)}})\\ ;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \arg \mathop {\max }\limits_\theta \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log } (P(Y|Z,\theta )P(Z{\rm{|}}\theta ))\\ ;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \arg \mathop {\max }\limits_\theta \sum\limits_Z {P(Z|Y,{\theta ^{(i)}})\log } (P(Y,Z|\theta ))\\ ;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \arg \mathop {\max }\limits_\theta Q(\theta ,{\theta ^{(i)}}) \end{array}$$

算法描述如下，

输入：观测变量数据Y，隐变量数据Z，联合分布$P(Y,Z$ |$\theta )$ ,条件分布$P(Z$ | $Y,\theta )$； 输出：模型参数$\theta$。 1. 选择参数的初值${\theta ^{(0)}}$，开始迭代； 2. E步：记${\theta ^{(i)}}$为第i次迭代参数$\theta$的估计值，在第i+1次迭代时，计算如下的式子， 这里的$P(Z$ | $Y,{\theta ^{(i)}})$是在给定观测数据Y和当前的参数估计${\theta ^{(i)}}$条件下的关于隐变量Z的条件概率分布； 3. M步：求使$Q(\theta ,{\theta ^{(i)}})$极大化的$\theta$，确定第i+1次迭代的参数估计值${\theta ^{(i + 1)}}$，$${\theta ^{(i + 1)}} = \arg \mathop {\max }\limits_\theta Q(\theta ,{\theta ^{(i)}})$$4.重复步骤2和步骤3，直到收敛。

EM算法的另一种推导

基于上述的分析过程，建立对数似然函数如下，
$$l(\theta ) = \sum\limits_{i = 1}^N {\log P(x|\theta )} = \sum\limits_{i = 1}^N {\log \sum\limits_z {P(x,z|\theta )} }$$
若${Q_i}$是z的某一个分布，则有，
$$\begin{array}{l} l(\theta ) = \sum\limits_{i = 1}^N {\log \sum\limits_z {P(x,z|\theta )} } \\ ;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{i = 1}^N {\log \sum\limits_{{z_i}} {P({x_i},{z_i}|\theta )} } \\ ;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{i = 1}^N {\log \sum\limits_{{z_i}} {{Q_i}({z_i})\frac{{P({x_i},{z_i}|\theta )}}{{{Q_i}({z_i})}}} } \\ ;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ge \sum\limits_{i = 1}^N {\sum\limits_{{z_i}} {{Q_i}({z_i})\log \frac{{P({x_i},{z_i}|\theta )}}{{{Q_i}({z_i})}}} } \end{array}$$

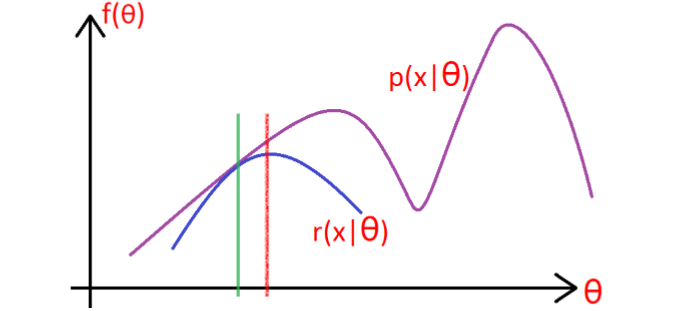
因为要找到尽量靠近的下界(图像性质可知)，所以就要使Jensen不等式的等号成立，则，
$$\frac{{P({x_i},{z_i}|\theta )}}{{{Q_i}({z_i})}} = c(c是常数)$$
进一步分析，
$$\begin{array}{l} \left. {\begin{array}{l} {{Q_i}({z_i}) \propto P({x_i},{z_i}|\theta )}\\ {\sum\limits_z {{Q_i}({z_i}) = 1} } \end{array}} \right}\\ \Rightarrow {Q_i}({z_i}) = \frac{{P({x_i},{z_i}|\theta )}}{{\sum\limits_z {P({x_i},{z_i}|\theta )} }}\\ ;;;;;;;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{P({x_i},{z_i}|\theta )}}{{P({x_i}|\theta )}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;;;;;;;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} = P({z_i}|{x_i},\theta ) \end{array}$$
所以，当且仅当${Q_i}$取上式的条件概率时，推导过程中的Jensen不等式才能取等号。

此时，EM算法描述为，

E步：对于每一个i，求， ${Q_i}({z^i}) = P({z_i}$ | ${x_i},\theta )$ M步：更新$\theta$

高斯混合模型(Gaussian Mixture Model,GMM)下的EM算法

首先，高斯混合分布如下，
$$p(x) = \sum\limits_{i = 1}^K {{\pi _i}p(x|{u_i},{\Sigma _i})}$$
该分布总共由K个高斯分布组成，这里的$p(x|{u_i},{\Sigma _i})$是多元高斯分布，
$$p(x) = \frac{1}{{{{(2\pi )}^{\frac{n}{2}}}{{\left| \Sigma \right|}^{\frac{1}{2}}}}}{e^{ – \frac{1}{2}{{(x – u)}^T}{\Sigma ^{ – 1}}(x – u)}}$$
而高斯混合分布中的${\pi _i}$为第i个混合成分的“混合系数”，且 $\sum\limits_{i = 1}^K {{\pi _i} = 1}$。

那么估计GMM的问题如下：已知随机变量X是由K个高斯分布混合而成，取各个高斯分布的概率为${\pi _1},{\pi _2}, \cdots ,{\pi _K}$，第i个高斯分布的均值为${u_i}$，方差为${\Sigma _i}$。若观测到随机变量的一系列样本为${x_1},{x_2}, \cdots ,{x_N}$，试估计参数$\theta = (\pi ,u,\Sigma )$。

应用EM算法来估计GMM的参数。
1.E步：
$$\begin{array}{l} {Q_i}({z^i}) = P({z_i}|{x_i},\theta )\\ ;;;;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{P({z_i},{x_i},\theta )}}{{P({x_i},\theta )}}\\ ;;;;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{P({x_i}|{z_i},\theta )P({z_i},\theta )}}{{P({x_i},\theta )}}\\ ;;;;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{P({x_i}|{z_i},\theta )P({z_i})}}{{P({x_i})}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;;;;;;;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{\pi _k}N({x_i}|{u_k},{\Sigma _k})}}{{\sum\limits_{j = 1}^K {{\pi _j}N({x_i}|{u_j},{\Sigma _j})} }} \end{array}$$
上式的含义为，样本${x_i}$由第k个高斯分布生成的概率，记作${\gamma _{ik}}$，则，
$${\gamma _{ik}} = \frac{{{\pi _k}N({x_i}|{u_k},{\Sigma _k})}}{{\sum\limits_{j = 1}^K {{\pi _j}N({x_i}|{u_j},{\Sigma _j})} }}$$
2.M步：将高斯分布带入计算，

$$\begin{array}{l} \sum\limits_{i = 1}^N {\sum\limits_{{z_i}} {{Q_i}({z_i})\log \frac{{P({x_i},{z_i}|\pi ,u,\Sigma )}}{{{Q_i}({z_i})}}} } \\ = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{Q_i}({z_i} = j)} } \log \frac{{P({x_i}|{z_i} = j,\theta )P({z_i} = j|\theta )}}{{{Q_i}({z_i} = j)}}\\ = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{\gamma _{ij}}\log \frac{{\frac{1}{{{{(2\pi )}^{\frac{n}{2}}}{{\left| {{\Sigma _j}} \right|}^{\frac{1}{2}}}}}\exp ( – \frac{1}{2}{{({x_i} – {u_j})}^T}\Sigma _j^{ – 1}({x_i} – {u_j})) \cdot {\pi _j}}}{{{\gamma _{ij}}}}} } \end{array}$$

对均值求偏导，
$${\nabla _{{u_l}}} = \sum\limits_{i = 1}^N {{\gamma _{il}}\Sigma _l^{ – 1}({x_i} – {u_l})} = 0$$则其均值为，
$${u_l} = \frac{{\sum\limits_{i = 1}^N {{\gamma _{il}}{x_i}} }}{{\sum\limits_{i = 1}^N {{\gamma _{il}}} }}$$
对方差求偏导
$${\nabla _{{\Sigma _l}}} = – \frac{1}{2}\sum\limits_{i = 1}^N {{\gamma _{il}}(\frac{1}{{{\Sigma _l}}} – \frac{{({x_i} – {u_l}){{({x_i} – {u_l})}^T}}}{{\Sigma _l^2}})} = 0$$则其方差为，
$${\Sigma _l} = \frac{{\sum\limits_{i = 1}^N {{\gamma _{il}}({x_i} – {u_l}){{({x_i} – {u_l})}^T}} }}{{\sum\limits_{i = 1}^N {{\gamma _{il}}} }}$$
对$\pi$的求解，使用拉格朗日乘子法，考虑$\sum\limits_{j = 1}^K {{\pi _j} = 1}$，$$L(\pi ) = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{\gamma _{ik}}\log {\pi _j} + \beta (\sum\limits_{j = 1}^K {{\pi _j} – 1} )} }$$
对${\pi _j}$求导，
$$\begin{array}{l} \frac{{\partial L}}{{\partial {\pi _j}}} = \sum\limits_{i = 1}^N {\frac{{{\gamma _{ij}}}}{{{\pi _j}}} + \beta = 0} \\ {\pi _j} = \sum\limits_{i = 1}^N {\frac{{{\gamma _{ij}}}}{{ – \beta }}} \\ \sum\limits_{j = 1}^K {{\pi _j} = \sum\limits_{j = 1}^K {\sum\limits_{i = 1}^N {\frac{{{\gamma _{ij}}}}{{ – \beta }}} } } \\ ;;;;;;;;;; = \frac{1}{{ – \beta }}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^K {{\gamma _{ij}}} } \\ ;;;;;;;;;; = \frac{1}{{ – \beta }}\sum\limits_{i = 1}^N 1 \\ ;;;;;;;;;; = \frac{1}{{ – \beta }}N = 1\\- \beta = N\\{\pi _j} = \sum\limits_{i = 1}^N {\frac{{{\gamma _{ij}}}}{{ – \beta }}} = \frac{{\sum\limits_{i = 1}^N {{\gamma _{ij}}} }}{N} \end{array}$$

3. 重复以上的计算，直到对数似然函数不再有明显变化为止。

总结估计GMM参数的EM算法如下：

输入：观测数据${x_1},{x_2}, \cdots ,{x_N}$，高斯混合模型 输出：高斯混合模型参数$\theta = (\pi ,u,\Sigma )$ 1. 取参数的初始值开始迭代 。 2. E步：计算当前模型参数，即第i个样本${x_i}$由第k个高斯分布生成的后验概率 3. M步：计算新一轮的模型参数 4.重复第2步和第3步，直到收敛。

高斯混合模型(Gaussian Mixture Model,GMM)下的EM算法——举例说明

下面举个例子来说明一下，

已知男生和女生的身高服从高斯分布，其中男生身高服从参数为$({u_1},\sigma _1^2)$的高斯分布，女生身高服从参数为$({u_2},\sigma _2^2)$的高斯分布，现在已知N个样本的观测值为${x_1},{x_2}, \cdots ,{x_N}$，但是不知道这些身高值代表的是男还是女，如果用${\pi _1}$表示这些数据来自高斯分布$N({u_1},\sigma _1^2)$的概率，用${\pi _2}$表示这些数据来自高斯分布$N({u_2},\sigma _2^2)$的概率。那么用观测样本来估计参数${\theta _k} = ({\pi _k},{u_k},\sigma _k^2),k = 1,2$的值。

那么这其实就是一个一元的高斯混合模型。可采用如下方式来求解。
1.先猜测参数值
$\begin{array}{l} 男：{u_1} = 1.75,\sigma _1^2 = 50,{\pi _1} = 0.5\\ 女：{u_2} = 1.62,\sigma _2^2 = 30,{\pi _2} = 0.5 \end{array}$
这一步相当于EM算法中的第一步，设置参数的初始值。
2.
2.1假设${x_1} = 1.84$，那么使用高斯概率密度函数可以算出${p_1},{p_2}$，此时又已知${\pi _1},{\pi _2}$(第一步猜测的值)，所以，可以算出该样分别属于男生和女生的概率，即，
$$\begin{array}{l} P(1,男) = \frac{{{p_1}{\pi _1}}}{{{p_1}{\pi _1} + {p_2}{\pi _2}}}\\ P(1,女) = \frac{{{p_2}{\pi _2}}}{{{p_1}{\pi _1} + {p_2}{\pi _2}}} \end{array}$$
其实这一步就是EM算法里求${\gamma _{ik}}$，即相当于EM算法中的E步。
这里假设算出来$P(1,男) = {\rm{0}}{\rm{.8,}}P(1,女) = 0.2$。

2.2那么再来算一个值，即${x_1} = 1.84$这个样本属于男性和女性的数据
$$\begin{array}{l} {x_1}(男) = {\rm{0}}{\rm{.8*1}}{\rm{.84 = 1}}{\rm{.472}}\\ {x_1}(女) = {\rm{0}}{\rm{.2*1}}{\rm{.84 = 0}}{\rm{.368}} \end{array}$$
对于上面结果的解释，可以认为${x_1} = 1.84$这个样本其中有1.472的部分属于男性，有0.368的部分属于女性，当然这仅仅是从数学层面上来解释。

2.3 重复上述过程，直到第N个样本，这样就能得到一系列如下的值，
$$P(i,男)P(i,女),{x_i}(男),{x_i}(女),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;;;i = 1,2, \cdots ,N$$

3.更新参数
这里的均值为
$${u_1} = \frac{{{x_1}(男){\rm{ + }}{x_2}(男){\rm{ + }} \cdots {\rm{ + }}{x_N}(男)}}{{P(1,男) + P(2,男){\rm{ + }} \cdots {\rm{ + }}P(N,男)}}$$$${u_2} = \frac{{{x_1}(女){\rm{ + }}{x_2}(女){\rm{ + }} \cdots {\rm{ + }}{x_N}(女)}}{{P(1,女) + P(2,女){\rm{ + }} \cdots {\rm{ + }}P(N,女)}}$$
方差为，
$$\begin{array}{l} \sigma _{\rm{1}}^{\rm{2}}{\rm{ = }}\frac{{P({\rm{1,男}})}}{{\sum\limits_{j = 1}^N {P(j,男)} }}{({x_1} – {u_1})^2}{\rm{ + }}\frac{{P({\rm{2,男}})}}{{\sum\limits_{j = 1}^N {P(j,男)} }}{({x_{\rm{2}}} – {u_1})^2}{\rm{ + }} \cdots {\rm{ + }}\frac{{P(N{\rm{,男}})}}{{\sum\limits_{j = 1}^N {P(j,男)} }}{({x_N} – {u_1})^2}\\ \sigma _2^{\rm{2}}{\rm{ = }}\frac{{P({\rm{1,女}})}}{{\sum\limits_{j = 1}^N {P(j,女)} }}{({x_1} – {u_{\rm{2}}})^2}{\rm{ + }}\frac{{P({\rm{2,女}})}}{{\sum\limits_{j = 1}^N {P(j,女)} }}{({x_{\rm{2}}} – {u_{\rm{2}}})^2}{\rm{ + }} \cdots {\rm{ + }}\frac{{P(N{\rm{,女}})}}{{\sum\limits_{j = 1}^N {P(j,女)} }}{({x_N} – {u_{\rm{2}}})^2} \end{array}$$
混合系数为，
$$\begin{array}{l} {\pi _{\rm{1}}}{\rm{ = }}\frac{{\sum\limits_{{\rm{i}} = 1}^N {P(i,男)} }}{{\sum\limits_{{\rm{i}} = 1}^N {P(i,男)} + \sum\limits_{{\rm{i}} = 1}^N {P(i,女)} }} = \frac{{\sum\limits_{{\rm{i}} = 1}^N {P(i,男)} }}{N}\\ {\pi _2}{\rm{ = }}\frac{{\sum\limits_{{\rm{i}} = 1}^N {P(i,女)} }}{{\sum\limits_{{\rm{i}} = 1}^N {P(i,男)} + \sum\limits_{{\rm{i}} = 1}^N {P(i,女)} }} = \frac{{\sum\limits_{{\rm{i}} = 1}^N {P(i,女)} }}{N} \end{array}$$
这一步其实就是EM算法中的M步，参数更新式。