Dijkstra算法即迪杰斯特拉算法,用于解决赋权有向图的单源最短路径问题。单源最短路径即起点确定,到图中任意节点的最短路径。
算法描述:
使用两个集合C、U分别容纳已找出最短路径的节点和未确定最短路径的节点。起始状态下,集合C只有起始节点,集合U包含其他所有节点。然后从起始节点开始图遍历寻找到每一节点的最短路径。每找到一个最短路径,就将该节点(K)加入到集合C,并从集合U移除。然后使用新加入到C的节点K来更新集合U,并找到下一个最短路径,再加入到集合C并从集合U移除,重复此过程,直到找到全部最短路径。
模型:两个集合
- 已找到最短路径的节点集合
初始状态下该集合中只有起点一个元素
- 未找到最短路径的节点集合
初始状态下该集合中包含除起点之外的其他全部节点
具体操作:
1、集合初始化
C:节点表示为节点号、路径、路径长度
U:节点表示为和源节点中新加入节点的权值,相邻则记为其权值,否则为无穷大(只是一个记号)表示两个节点不相邻
2、集合更新
将U中路径权值最小的节点取出放入集合C中,记为节点K,使用K更新集合U中的节点权值
3、迭代处理
重复过程2,直到全部节点的最短路径已找出
4、结束
输出集合C
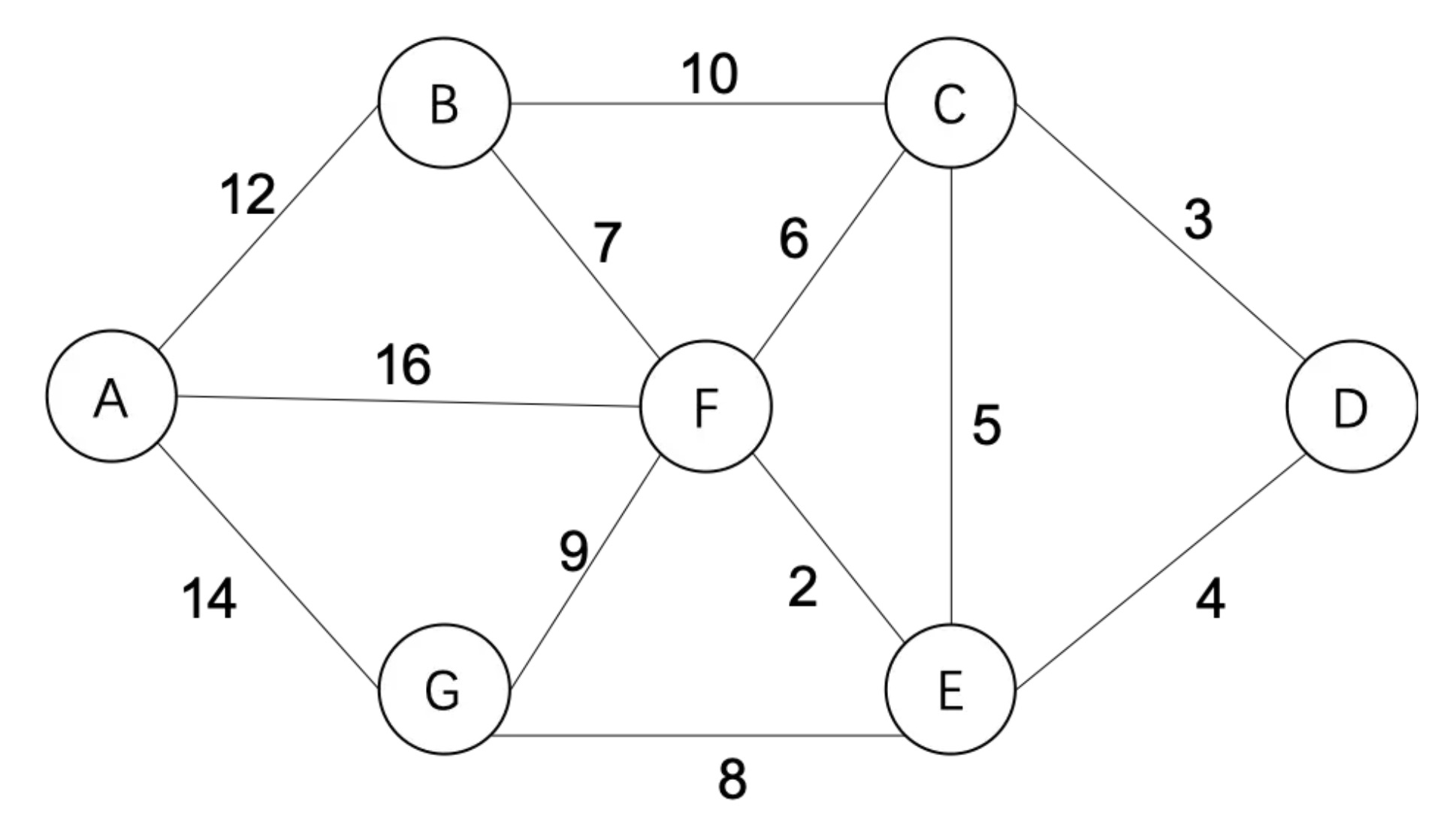
Java实现
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
2
3 //记录节点名称和对应的索引编号
4 static Map<String, Integer> map = new HashMap<>(7);
5
6 static {
7 map.put("A", 0);
8 map.put("B", 1);
9 map.put("C", 2);
10 map.put("D", 3);
11 map.put("E", 4);
12 map.put("F", 5);
13 map.put("G", 6);
14 }
15
16 public static void main(String[] args) {
17
18 //记录顶点之间的连接关系及其权重长度
19 List<Edge> list = new ArrayList<>();
20 list.add(new Edge("A", "B", 12));
21 list.add(new Edge("A", "F", 16));
22 list.add(new Edge("A", "G", 14));
23 list.add(new Edge("B", "C", 10));
24 list.add(new Edge("B", "F", 7));
25 list.add(new Edge("C", "D", 3));
26 list.add(new Edge("C", "E", 5));
27 list.add(new Edge("C", "F", 6));
28 list.add(new Edge("D", "E", 4));
29 list.add(new Edge("E", "F", 2));
30 list.add(new Edge("E", "G", 8));
31 list.add(new Edge("F", "G", 9));
32
33 Graph graph = new Graph(list, map.size());
34
35 String start = "D";
36 System.out.println("以" + start + "为起点深度优先遍历:");
37 graph.dfs(map.get(start));
38 System.out.println();
39
40 int[][] matrix = graph.getMatrix();
41
42 //分别表示已找到最短路径集合C和未找到最短路径集合U
43 List<Tuple3<String, Integer, String>> C = new ArrayList<>(7);
44 List<Tuple3<String, Integer, String>> U = new ArrayList<>(7);
45 //迪杰斯特拉算法
46 //初始化
47 String initNode = "D";
48 int i = map.get(initNode);
49 C.add(new Tuple3(initNode, 0, initNode));//集合C中只有起始节点,其最短距离为0
50 //集合U中包含除起始节点外的所有其他节点,和起始节点相邻则距离为权重,否则距离初始化为无穷大
51 for (String key : map.keySet()) {
52 // 排除初始节点
53 if (!key.equals(initNode)) {
54 int j = map.get(key);
55 if (matrix[i][j] != Integer.MAX_VALUE) {
56 //如果和初始节点相邻,则添加其距离,否则不可达
57 U.add(new Tuple3(key, matrix[i][j], initNode + "->" + key));
58 } else {
59 U.add(new Tuple3(key, Integer.MAX_VALUE, "N/A"));
60 }
61 }
62 }
63 //集合更新
64 updateCollection(C, U, map, matrix);
65
66 System.out.println("以" + initNode + "为起点到其它各顶点的最短路径及路径长度:");
67 for (Tuple3<String, Integer, String> tuple3 : C) {
68 System.out.println(initNode + "到" + tuple3._1() + " path: " + tuple3._3() +
69 " weight: " + tuple3._2());
70 }
71 }
72
73 /**
74 * 注:不考虑路径相同的情况
75 * @param C 已找到最短路径的集合
76 * @param U 未找到最短路径的集合
77 * @param map 用于记录顶点和索引的对应关系
78 * @param matrix 这里表示无向图的邻接矩阵
79 */
80 public static void updateCollection(List<Tuple3<String, Integer, String>> C,
81 List<Tuple3<String, Integer, String>> U, Map<String, Integer> map, int[][] matrix) {
82 //直到都找到最短路径后退出,此时集合C已容纳全部节点
83 if (C.size() == map.size()) {
84 return;
85 }
86 //先通过集合C中的新加入节点更新集合U中的距离
87 Tuple3<String, Integer, String> K = C.get(C.size() - 1);
88 int i = map.get(K._1());//集合中K的节点索引编号
89 int distance = K._2();//K到初始节点的距离
90 Tuple3<String, Integer, String> temp = U.get(0);//取更新后的集合U中的最小距离节点
91 // 遍历集合U,对路径长度进行更新
92 for (int x = 0; x < U.size(); x++) {
93 Tuple3<String, Integer, String> tup = U.get(x);
94 int j = map.get(tup._1());//节点索引
95 int dis = tup._2();//到初始节点的距离
96 // 如果和节点K相邻,则更新最短距离 例如AB=5 AC=8 BC=1,那么在B加入集合C后,
97 // 就要更新A到C的最短路径从A->C 8 变成 A->B->C 6
98 if (matrix[i][j] != Integer.MAX_VALUE) {
99 int newdis = distance + matrix[i][j];
100 if (newdis < dis) {
101 U.set(x, new Tuple3(tup._1(), distance + matrix[i][j], K._3() + "->" + tup._1()));
102 }
103 }
104
105 //找到路径最短的那个节点
106 if (U.get(x)._2() < temp._2()) {
107 temp = U.get(x);
108 }
109 }
110 C.add(temp);//将已找到最短路径的节点加入到集合C中
111 U.remove(temp);//将已找到最短路径的节点从集合U中删除
112 //迭代更新步骤
113 updateCollection(C, U, map, matrix);
114 }
115
116 static class Graph {
117
118 int size;//顶点数
119 int[][] matrix;//邻接矩阵
120 int[] visited;//节点已遍历标记
121
122 public Graph(List<Edge> edges, int size) {
123 this.size = size;
124 matrix = new int[size][size];
125 visited = new int[size + 1];
126 for (int i = 0; i < size; i++) {
127 for (int j = 0; j < size; j++) {
128 if (i == j) {
129 matrix[i][j] = 0;
130 } else {
131 matrix[i][j] = Integer.MAX_VALUE;
132 }
133 }
134 }
135 for (Edge edge : edges) {
136 int i = map.get(edge.getNode1());
137 int j = map.get(edge.getNode2());
138 matrix[i][j] = edge.getWeight();
139 //无向图
140 matrix[j][i] = edge.getWeight();
141 }
142 }
143
144 /**
145 * 深度优先遍历
146 * @param start 起始节点
147 */
148 void dfs(int start) {
149 System.out.print(getNodeName(start) + " ");
150 visited[start] = 1;
151 for (int j = 0; j < this.size; j++) {
152 if (matrix[start][j] != Integer.MAX_VALUE && visited[j] != 1) {
153 dfs(j);
154 }
155 }
156 }
157
158 /**
159 * 根据索引,获取节点名称
160 * @param index
161 * @return
162 */
163 String getNodeName(int index) {
164 for (Entry<String, Integer> entry : map.entrySet()) {
165 if (entry.getValue() == index) {
166 return entry.getKey();
167 }
168 }
169 return null;
170 }
171
172 public int[][] getMatrix() {
173 return matrix;
174 }
175
176 }
177
178 static class Edge {
179
180 String node1;//节点名
181 String node2;//节点名
182 int weight;//节点1和2的路径权重
183
184 public Edge(String node1, String node2, int weight) {
185 this.node1 = node1;
186 this.node2 = node2;
187 this.weight = weight;
188 }
189
190 public String getNode1() {
191 return node1;
192 }
193
194 public String getNode2() {
195 return node2;
196 }
197
198 public int getWeight() {
199 return weight;
200 }
201 }
202}
203
204
示例输出
2
3
4
5
6
7
8
9
10
11
12
2D C B A F E G
3以D为起点到其它各顶点的最短路径及路径长度:
4D到D path: D weight: 0
5D到C path: D->C weight: 3
6D到E path: D->E weight: 4
7D到F path: D->E->F weight: 6
8D到G path: D->E->G weight: 12
9D到B path: D->C->B weight: 13
10D到A path: D->E->F->A weight: 22
11
12
总结
起点明确这个很重要。文中有深度优先遍历的实现和输出(图构建测试用),广度优先遍历也很简单,而且本文所描述的算法其思想也是广度优先。每次先考虑相邻情况,用相邻关系中的最短路径来制造一个新的最短路径,并用于更新其他路径的长度。
