克鲁斯卡尔算法
克鲁斯卡尔算法求最小生成树
应用场景——公交站问题
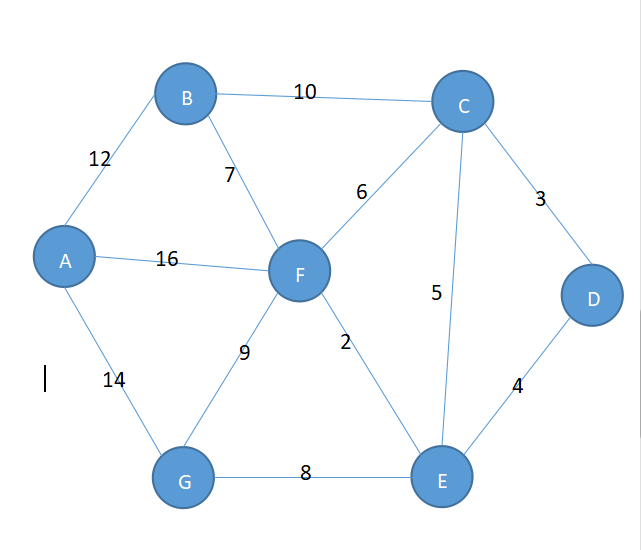
- 某城市新增7个站点(A,B,C,D,E,F,G)现在需要修路将七个站点连通
- 各站点的距离用边线表示(权),比如A—B距离12公里
- 问:如何修路保证每个站点都能连通,并且总的修建公路里程最短?
克鲁斯卡尔算法介绍
- 克鲁斯卡尔算法,是用来求加权连通图的最小生成树的算法。
- 基本思路:按照权值从大到小的顺序选择(n – 1)条边,并保证这(n – 1)条边不构成回路
- 具体做法:首先构造一个只含n个顶点的森林,然后依权值从小到大从连通网中选择边加入到森林中去,并使森林中不产生回路,直至森林变成一棵树为止。
图解克鲁斯卡尔算法
构成回路定义
- 构成回路的条件:边的两个顶点指向同一个终点。
- 终点定义:就是将所有的顶点按照从小到大的顺序排好之后,某个顶点的终点就是“与他连通的最大的顶点”,看一条边的两个端点的终点是要分离开再看。
如何判定某点的终点
在上述图片上的所有节点按照从小到大的顺序排列为:A,B,C,D,E,F,G,
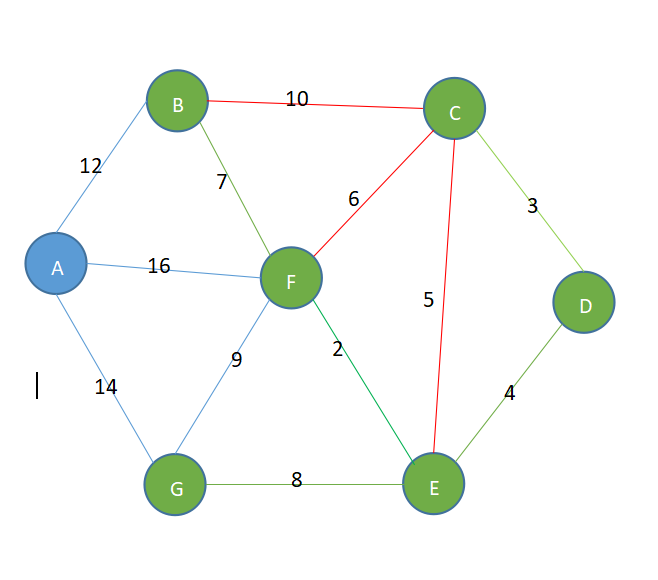
前提:下图中绿色线表示已经连接,绿色节点表示已经被选中访问,是选中的节点。
在下图中中添加,单独看D点和E点,D点仅与C点相联,终点是D点,E点与F点相联,终点是F点,终点不一样,可以连接。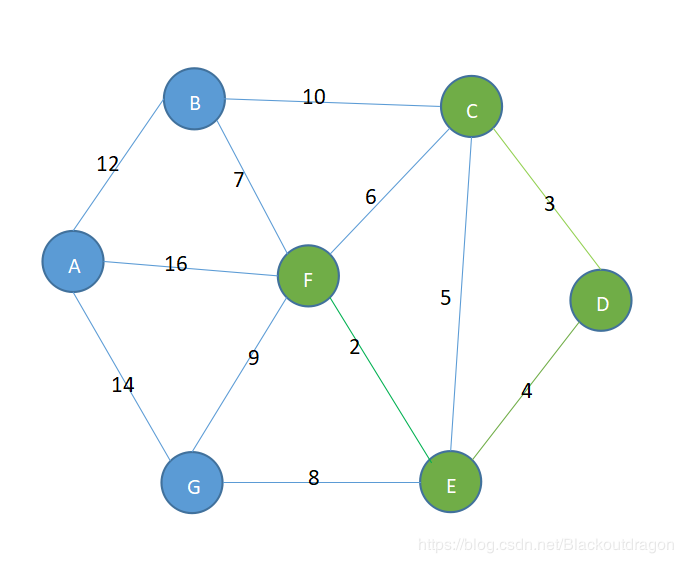
在下图中如果要添加,未添加之前,单独看结点C,按照对应的顺序,C点是可以到达对应的F点,故而C点的终点是F点,E点也是可以到达F点,所以F点的终点也是F点,所以不能添加.。同理不能添加。
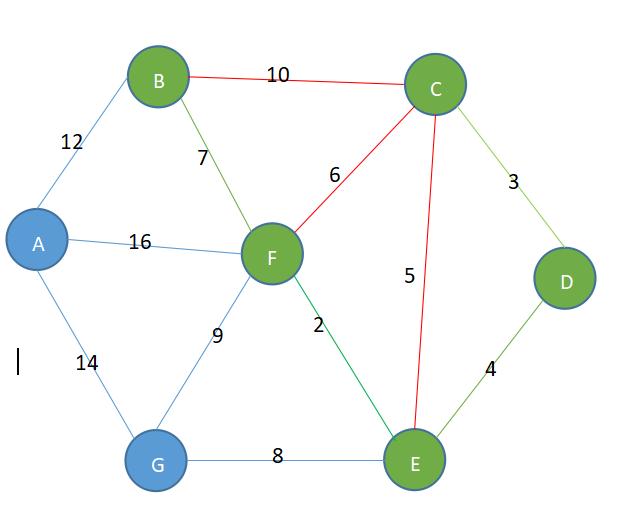
图解步骤
- 将所有的边,根据权值进行排列,选取权值最小的边2
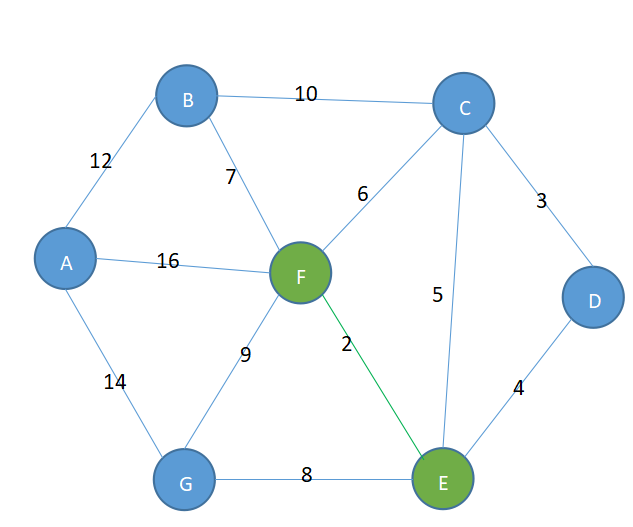
- 在不构成回路的情况下,在剩余的边中选取权值最小的边3
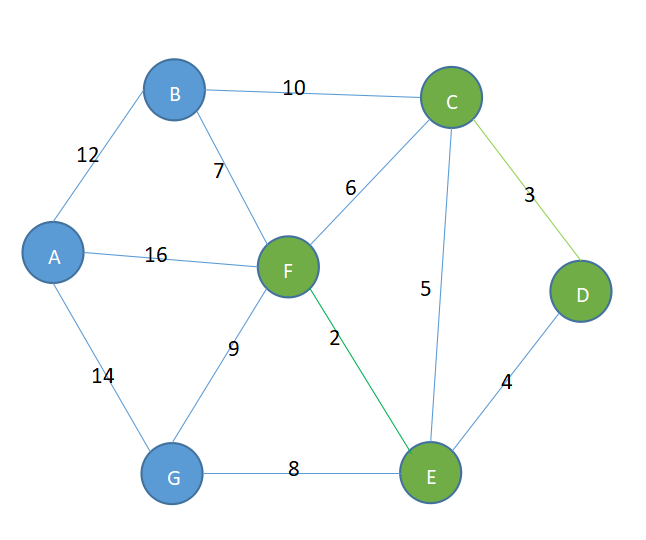
- 在不构成回路的情况下,在剩余的边中选择权值最小的边4
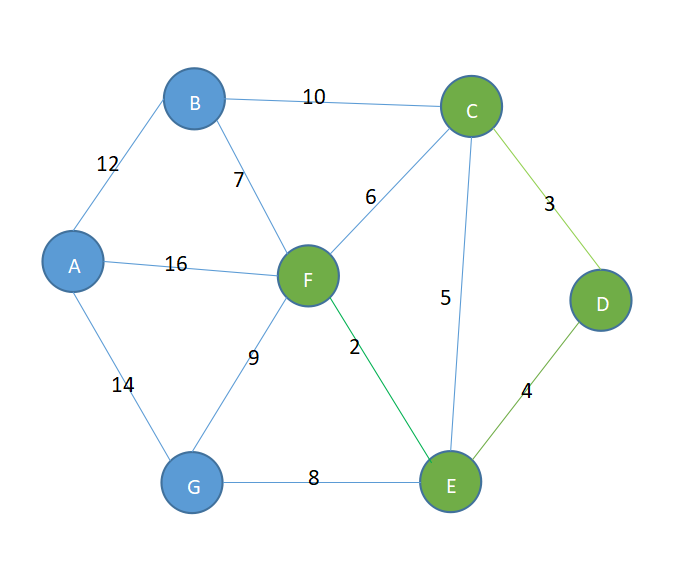
- 虽然在剩余的边中5和6都比较小,但是两者都会构成回路,所以排除,仅可以选择7

- 在不构成回路的情况下,选择剩余边中权最小的值8

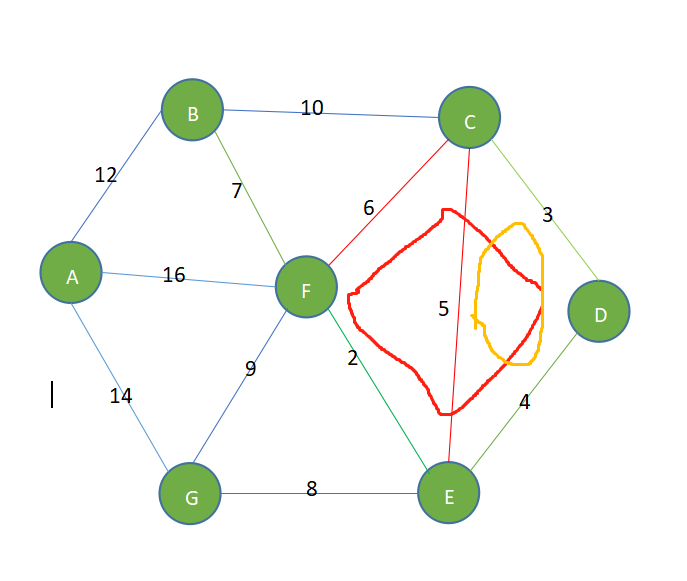
- 在剩余的边中,选择权值最小,同时又不会构成回路的边。9,10,与会构成回路,故而不选,所以选择12.图中红线所连即为最小生成树。
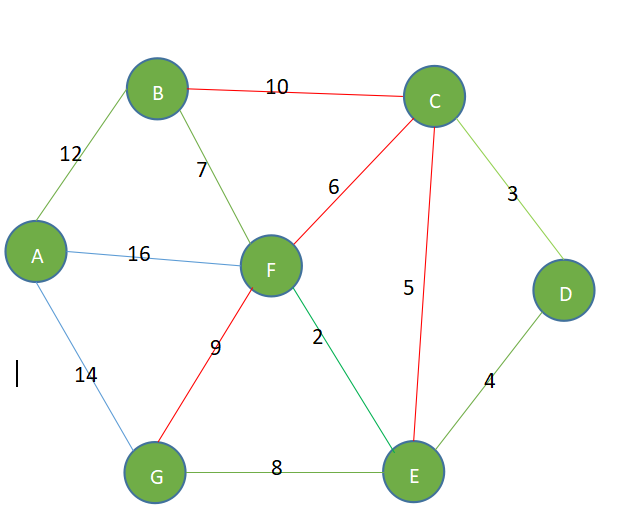
- 结果为:2,3,4,7,8,12,总共权值为:36,绿线为对应的选中的路径
代码实现
-
根据思路分析,添加一条边要考虑权值,考虑两边的端点,构建一个有关边的类EDate,能够获取边的两个端点和权值
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2 char start;
3 char end;
4 //分别定义边的两个端点
5 int weight;
6 //定义相关的权值
7
8 public EDate(char start, char end, int weight) {
9 this.start = start;
10 this.end = end;
11 this.weight = weight;
12 }
13
14 @Override
15 public String toString() {
16 return "边{" +
17 "start=" + start +
18 ", end=" + end +
19 ", weight=" + weight +
20 '}' + "\n";
21 }
22}
23
24
- 将原图中边全部转成对应的有关边的类EDate,生成对应的数组,然后将数组进行从小到大的排序,以确保遍历时从小到大
注意,我们在将边形成相关的类时,仅仅去上三角,确保不重复,同时保证边的两端点是按照固定的顺序
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
2 * 将图中所有的边获取,转成对应的数组进行排序
3 *
4 * @return 有几个问题,第一个对于无向图而言,他是邻接矩阵,那就意味着双向边,那么每一次都得保存两个边
5 * 对称矩阵,那就取上三角,减少重复的
6 * 第二个问题:整个排序的过程中,已经排过序的那就删除,即使是最小的也要删除
7 */
8 private EDate[] getEdges() {
9 int index = 0;
10 EDate[] edges = new EDate[edgenum];
11 for (int i = 0;i < vertex.length;i ++){
12 for(int j = i + 1;j < vertex.length;j ++){
13 if(matrix[i][j] != INF){
14 edges[index] = new EDate(vertex[i],vertex[j],matrix[i][j]);
15 index ++;
16 }
17 }
18 }
19
20 return edges;
21 //对已经生成的数据进行排序
22 }
23
24 /**
25 *
26 * @param edge 对传入边构成的数组进行排序
27 */
28 public void kruscalSort(EDate[] edge){
29 EDate temp;
30 for(int i = 0;i < edge.length;i ++){
31 for(int j = 0;j < edge.length - 1 - i;j ++){
32 if (edge[j].weight > edge[j + 1].weight){
33 temp = edge[j];
34 edge[j] = edge[j + 1];
35 edge[j + 1] = temp;
36 }
37 }
38 }
39 }
40
41
-
生成对应的终点数组,每一个节点的索引对应终点数组对应索引的值,该值为当前该节点对应的终点,初始都为零,随着添加而发生变化,逐渐调整
-
获取当前节点在对应的节点数组中对应的索引,因为判定终点是按照节点的固定顺序进行判定组合,所以必须获取当前的索引,并且判定节点
2
3
4
5
6
7
8
9
10
11
2 private int getPosition(char ch) {
3 for (int i = 0; i < vertex.length; i++) {
4 if (vertex[i] == ch) {
5 return i;
6 }
7 }
8 return -1;
9 }
10
11
-
生成对应的终点索引
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2 * 功能:用于获取当前节点的对应的终点
3 * @param end 数组记录的是各个顶点对应的重点是哪一个,是在遍历的过程中逐步形成的
4 * @param i 传入的是当前顶点对应的下标
5 * @return 返回的是下标为i这个顶点对应的重点的下标
6 */
7 public int getEnd(int[] end,int i){
8 while (end[i] != 0){
9 //不等于0,说明他还有下一个终点
10 i = end[i];
11 }
12 //等于0,说明已经没有了终点,本身就是终点
13 return i;
14 }
15
16
图解
初始条件,终点的数组索引对与端点的数组索引相对,若对应端点的索引在对应的索引的终点数组中数值为0,那就说明节点为本身,就返回自己的索引。否则为相应终点的对应索引
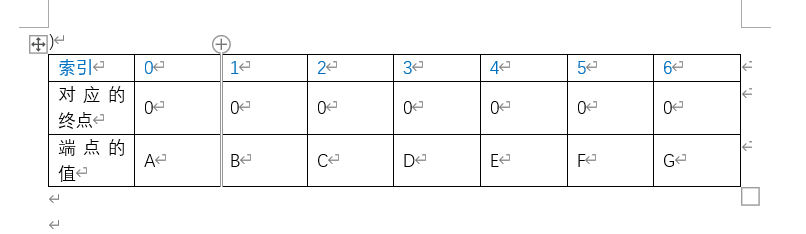
- 判定第一条边时,边{start=E, end=F, weight=2},
,E的索引为4,4对应的终点数组中的值为0,说明终点为自己,所以返回自己对应的索引4;F的索引为5,5对应的终点数组中的终点值为0,说明终点为自己,所以返回自己对应的索引5。而这不相同,所以可以添加对应节点的边。
在添加边的过程中,由于是读取上三角,意味着边的start小于end,所以将start在终点数组中终点的值设置为end对应的索引。而,5对应的终点的值仍旧是0,说明5对应的终点仍旧是本身。
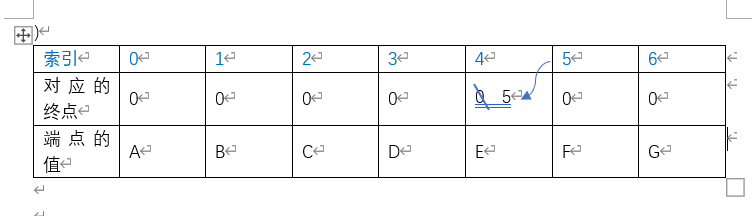
- 在添加边{start=C, end=D, weight=3}时,端点C在端点数组中对应的是2,2在终点数组中对应的值为0,所以终点为自身,所以返回的索引为2;同理可得端点D的终点值返回为3。然后添加对应的边,将C的终点值设置为D
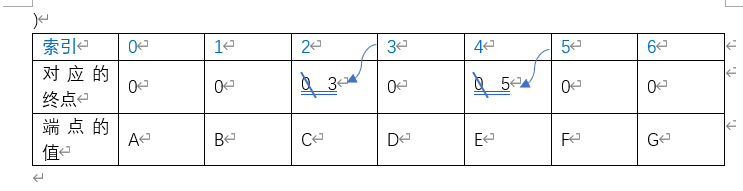
- 添加边{start=C, end=E, weight=5}时,端点C在端点数组中对应的索引为2,2在终点数组中对应的值为3,3在终点数组中的值对应为0,所以返回3,即C对应的终点为D;端点D同理可得,对应的终点值为5,即其终点为F。然后终点不一,添加对应的边CE,并将索引3在终点数组中对应的值改为D对应的终点值5
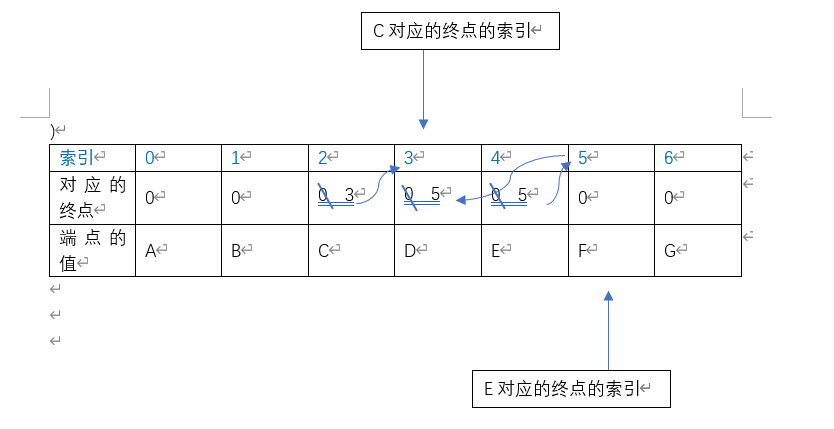
- 添加边{start=C, end=F, weight=6},端点C的索引在终点数组中对应的索引为5;端点F的索引在终点数组中对应的索引为0,如返回其本身,返回的值为5。两者相同,所以该边不可以添加。
- 添加边{start=B, end=F, weight=7},端点B的索引在终点数组中的对应的值是0,故而返回自己对应的索引1。端点F的终点由表可得为5。所以可以添加对应的边。
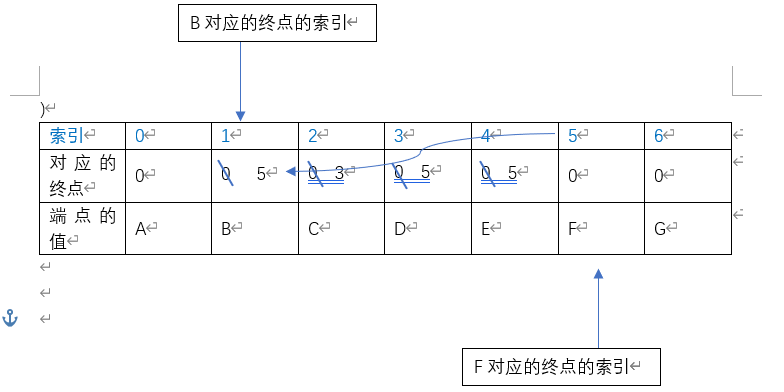
- 添加边{start=E, end=G, weight=8},端点E对应的索引为4,4在对应终点数组对应的值为5,由5在终点数组中对应的值为F,F对应的终点值为0,所以返回当前的值5。端点G对应的索引为6,6在对应的终点数组中对应的值为0,所以返回当前的索引6。故而,E的终点为F,G的终点为自身,不同,添加边EG,并将F的终点修改为6.
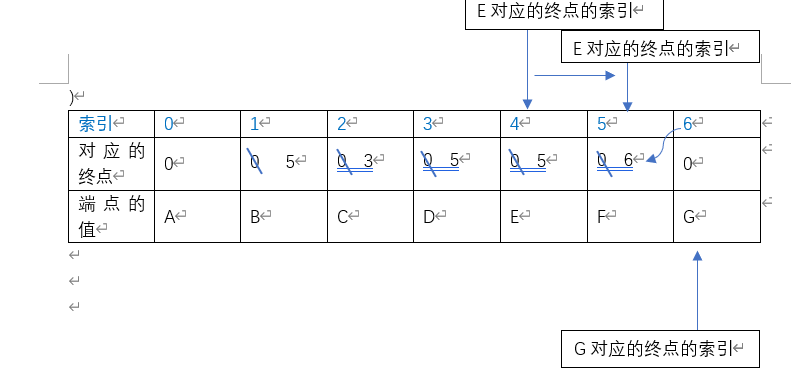
- 在添加边{start=F, end=G, weight=9},F点对应的终点为6,G对应的终点为6,相同,不可以添加。
- 在添加边{start=B, end=C, weight=10},B点对应的终点数组的值为5,将索引跳转到5处,5对应的索引为6,在跳转到6处,为0,返回当前索引为6。C对应的终点数组值为3,跳转到3的位置,3对应的值为5,5对应的值为6,6对应的值为0,返回当前索引6。二者相同,不可以添加。
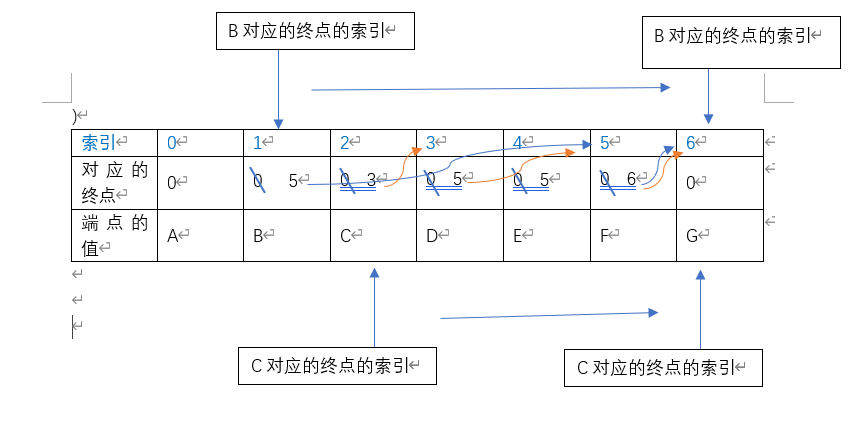
- 添加边{start=A, end=B, weight=12},A的终点为0当前值0,B由上可知,对应的终点为G,二者不同可添加对应的边。将A的终点值设置为6,即其终点为G。
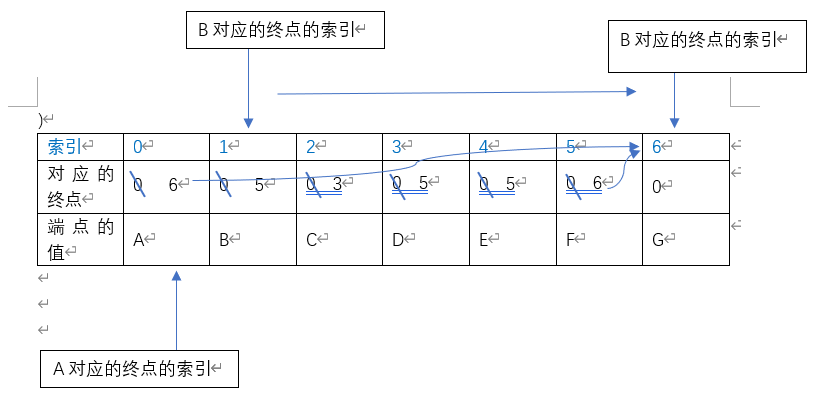
- 添加边{start=A, end=G, weight=14},A的终点为G,G的终点是自身,所以二者相同不可以添加。
- 添加边{start=A, end=F, weight=16},端点A的终点为F,F的终点是G,所以二者相同,不可以添加。
总的流程,生成对应的边类型对应的数组,然后从小到大进行排序,并从小到大进行添加,再添加的过程中获取对应的顶点的终点值,并比较二者是否相同
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2 int index = 0; //表示最后结果数组的索引
3 int[] ends = new int[vertex.length]; //用于保存“已有最小生成树”中的每个顶点在最小生成树中的终点
4 //问题:我的想法是什么,每一个节点都有一个对应的终点的地图,然后每一次都要遍历
5 EDate[] res = new EDate[edgenum]; //创建结果数组,保存最终的最后的最小生成树
6
7 //获取图中所有的边的集合,一共有十二条边
8 EDate[] edges = getEdges();
9 kruscalSort(edges); //对已经有的数据进行排序
10 for(int i = 0;i < edges.length;i ++){
11 //判断要加入的边是否构成回路,如果构成回路,那就加入最终循环,如果没有加入,那就跳过
12
13 //第一部分,获取要添加边对应的顶点
14 int p1 = getPosition(edges[i].start);
15 int p2 = getPosition(edges[i].end);
16 //第二部分,判定对应的顶点是否已经在最小生成树中
17 int m = getEnd(ends,p1);
18 int n = getEnd(ends,p2);
19 //根据判定结果进行增加
20 if(m != n){
21 //说明不构成回路
22 ends[m] = n;
23 //设置m在已有最小生成树终点
24 res[index ++] = edges[i];//有一条边加入到result中
25 System.out.println(Arrays.toString(ends));
26 }
27 }
28 }
29
30
总的代码
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
2
3import java.util.Arrays;
4
5public class KruscalCase {
6
7 private int edgenum;//定义边的个数
8 private char[] vertex;//定义对应的节点数组
9 private int[][] matrix;//邻接数组保存对应的边
10 private static final int INF = Integer.MAX_VALUE;//用int的最大值表示没有连通的边
11
12 public static void main(String args[]) {
13 char[] vertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G' };
14 int[][] edge = {
15 {0, 12, INF, INF, INF, 16, 14},
16 {12, 0, 10, INF, INF, 7, INF},
17 {INF, 10, 0, 3, 5, 6, INF},
18 {INF, INF, 3, 0, 4, INF, INF},
19 {INF, INF, 5, 4, 0, 2, 8},
20 {16, 7, 6, INF, 2, 0, 9},
21 {14, INF, INF, INF, 8, 9, 0}
22 };
23 KruscalCase kruscalCase = new KruscalCase(vertex, edge);
24 kruscalCase.list();
25 kruscalCase.kruscal();
26 }
27
28 //构造器
29
30 /**
31 * 在保留原数组的情况进行生成
32 *
33 * @param vertex 传入对应的节点数据
34 * @param edge 传入对应的边的二维数组
35 */
36 public KruscalCase(char[] vertex, int[][] edge) {
37 int vertexLen = vertex.length;
38
39 //节点进行赋值
40 this.vertex = new char[vertexLen];
41 for (int i = 0; i < vertex.length; i++) {
42 this.vertex[i] = vertex[i];
43 }
44
45 //对边进行赋值
46 matrix = new int[vertexLen][vertexLen];
47 for (int i = 0; i < vertexLen; i++) {
48 for (int j = 0; j < vertexLen; j++) {
49 this.matrix[i][j] = edge[i][j];
50 if (edge[i][j] != INF && edge[i][j] != 0) {
51 this.edgenum++;
52 }
53 }
54 }
55 edgenum /= 2;
56 }
57
58 /**
59 * 遍历对应的邻接矩阵
60 */
61 public void list() {
62 System.out.println("对应的邻接矩阵为");
63 for (int i = 0; i < vertex.length; i++) {
64 for (int j = 0; j < vertex.length; j++) {
65 System.out.printf("%12d", matrix[i][j]);
66 }
67 System.out.println();
68 }
69 }
70
71 //根据输入的字符获取相关的索引,有就返回相关的索引,没有就返回-1
72 private int getPosition(char ch) {
73 for (int i = 0; i < vertex.length; i++) {
74 if (vertex[i] == ch) {
75 return i;
76 }
77 }
78 return -1;
79 }
80
81 /**
82 * 将图中所有的边获取,转成对应的数组进行排序
83 * @return
84 */
85 private EDate[] getEdges() {
86 int index = 0;
87 EDate[] edges = new EDate[edgenum];
88 for (int i = 0;i < vertex.length;i ++){
89 for(int j = i + 1;j < vertex.length;j ++){
90 if(matrix[i][j] != INF){
91 edges[index] = new EDate(vertex[i],vertex[j],matrix[i][j]);
92 index ++;
93 }
94 }
95 }
96
97 return edges;
98 //对已经生成的数据进行排序
99 }
100
101 /**
102 *
103 * @param edge 对传入边构成的数组进行排序
104 */
105 public void kruscalSort(EDate[] edge){
106 EDate temp;
107 for(int i = 0;i < edge.length;i ++){
108 for(int j = 0;j < edge.length - 1 - i;j ++){
109 if (edge[j].weight > edge[j + 1].weight){
110 temp = edge[j];
111 edge[j] = edge[j + 1];
112 edge[j + 1] = temp;
113 }
114 }
115 }
116 }
117
118 /**
119 * 功能:用于获取当前节点的对应的终点
120 * @param end 数组记录的是各个顶点对应的重点是哪一个,是在遍历的过程中逐步形成的
121 * @param i 传入的是当前顶点对应的下标
122 * @return 返回的是下标为i这个顶点对应的重点的下标
123 */
124 public int getEnd(int[] end,int i){
125 while (end[i] != 0){
126 i = end[i];
127 }
128 return i;
129 }
130
131 public void kruscal(){
132 int index = 0; //表示最后结果数组的索引
133 int[] ends = new int[edgenum]; //用于保存“已有最小生成树”中的每个顶点在最小生成树中的终点
134 //问题:我的想法是什么,每一个节点都有一个对应的终点的地图,然后每一次都要遍历
135 EDate[] res = new EDate[edgenum]; //创建结果数组,保存最终的最后的最小生成树
136
137 //获取图中所有的边的集合,一共有十二条边
138 EDate[] edges = getEdges();
139 kruscalSort(edges); //对已经有的数据进行排序
140 for(int i = 0;i < edges.length;i ++){
141 //判断要加入的边是否构成回路,如果构成回路,那就加入最终循环,如果没有加入,那就跳过
142
143 //第一部分,获取要添加边对应的顶点
144 int p1 = getPosition(edges[i].start);
145 int p2 = getPosition(edges[i].end);
146 //第二部分,判定对应的顶点是否已经在最小生成树中
147 int m = getEnd(ends,p1);
148 int n = getEnd(ends,p2);
149 //根据判定结果进行增加
150 if(m != n){
151 //说明不构成回路
152 ends[m] = n;
153 //设置m在已有最小生成树终点
154 res[index ++] = edges[i];//有一条边加入到result中
155 }
156 }
157
158 //统计并且打印最小生成树,输出rests数组
159 System.out.println("最小生成树为:" + Arrays.toString(res));
160 }
161
162}
163
164//创建一个边的相关类,用于对边进行排序
165class EDate {
166 char start;
167 char end;
168 //分别定义边的两个端点
169 int weight;
170 //定义相关的权值
171
172
173 public EDate(char start, char end, int weight) {
174 this.start = start;
175 this.end = end;
176 this.weight = weight;
177 }
178
179 @Override
180 public String toString() {
181 return "边{" +
182 "start=" + start +
183 ", end=" + end +
184 ", weight=" + weight +
185 '}' + "\n";
186 }
187}
188
189
分析与总结
- 查找的终点的方法我认为很巧妙,函数就一个出口,当且仅当对应终点的索引为0,才会输出索引,否则就相互连结,跳转。当今仅有一个值可以输出,那就意味着所有的点都已经相联了。
- 在生成对应的与边相关的类的数组时,充分利用了邻接数组的好处,对称矩阵,仅仅去上三角,确保前一个端点的索引小于后一个端点的索引。