问题背景
搜索引擎根据用户的查询，快速准确地从网络中找到用户最需要的网页。由于“网页数量大”和“网页质量参差不齐”，需要搜索引擎根据查询，对网页排序，根据“用户搜索目的”，将最符合用户需求的网页依次排在最前面。
在pagerank算法之前，搜索引擎主要根据“网页的关键词词频”排序。但该排序没考虑网页质量。网页排序的任务中，最核心的难点在于判别网页质量。在此背景下，借鉴“学术论文的质量判别引用方法”，基于“链接分析”的pagerank算法被提出了。即在使用搜索引擎时，保持网页与查询一定相关度的基础上，$PR$值可以提供不错的排序依据。
算法的基本思想
“互联网上的网页”——>“图的节点”
“网页的出链”——>“指向其他节点的一条有向边”
“网页的入链”——>“其他节点指向这个节点的有向边”
“整个网络”——>“一张有向图”
网页质量的评估遵循以下两个假设
（1）一个网页的入链越多，网页质量越高
（2）一个网页的入链网页质量越高，页面质量越高
随机游走模型
“事物当前的状态”只与“其上一个状态”有关，而与“其上一个状态之前的状态”无关
用户上网过程
（1）初始状态时，用户访问所有页面的概率是相同的
（2）每次访问后，用户会根据“此时该页面的出链”以相同的概率访问“链接所指向的页面”
用户上网过程的行为就像在有向图上随机游走，通过分析对这种随机游走的概率分析，得到用户上网时停留在哪个网页的概率大些，概率越大网页质量越高。
算法的数学模型
STEP1
假设网络里一共有$N$个网页，则在初始阶段用户访问每个网页的概率是$\displaystyle\frac{1}{N}$，假设网页之间的概率转移矩阵为$T$(其中$T[i][j]$表示由 网页$j$ 跳转至 网页$i$ 的概率)，则用户第$n$次跳转之后的概率分布：
$$V_n = T \cdot V_{n-1} = T^n \cdot V_0$$
当$n \rightarrow +\infty$，$T$满足以下3个条件：
（a）随机矩阵$T$的每个元素$T[i][j] \geq 0$，且所有列和为1，即$\sum\limits_{i=1}^n T[i][j]=1$；
（b）随机矩阵$T$是不可约的(强连通的)，即图中“任何一个节点”都可以达到“其他节点里的一个”(图里不存在 终止点-不指向任何节点 和 陷阱点-只指向自己的节点)；
（c）随机矩阵$T$是非周期的，若A是周期的则Markov链的状态是周期性变化的，
则$lim_{n \rightarrow +\infty} V_n$最终收敛，得到的向量$V_n$里的元素是每个网页的概率值，即每个网页的$PR$值。
数值计算过程，收敛条件：（1）每个网页的$PR$值前后误差 小于 自定义的误差阈值；（2）迭代次数 大于 自定义的迭代次数阈值。
STEP2
如果有终止点和陷阱点会怎么样？下面用一个计算实例说明：
case1:
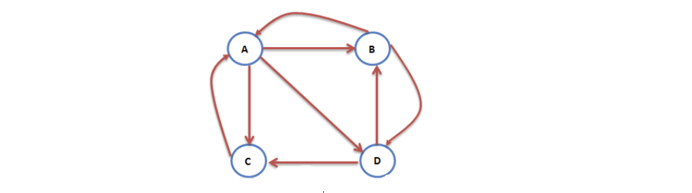$$V_0 = \left( \begin{matrix} \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \end{matrix} \right)， V_1 = T\cdot V_0 = \left( \begin{matrix} 0 & \displaystyle\frac{1}{2} & 1 & 0\ \displaystyle\frac{1}{3} & 0 & 0 & \displaystyle\frac{1}{2}\ \displaystyle\frac{1}{3} & 0 & 0 & \displaystyle\frac{1}{2}\ \displaystyle\frac{1}{3} & \displaystyle\frac{1}{2} & 0 & 0 \end{matrix} \right) \cdot \left( \begin{matrix} \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \end{matrix} \right) = \left( \begin{matrix} \displaystyle\frac{9}{24} \ \displaystyle\frac{5}{24} \ \displaystyle\frac{5}{24} \ \displaystyle\frac{5}{24} \end{matrix} \right)$$
$$\left( \begin{matrix} \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \end{matrix} \right)， \left( \begin{matrix} \displaystyle\frac{9}{24} \ \displaystyle\frac{5}{24} \ \displaystyle\frac{5}{24} \ \displaystyle\frac{5}{24} \end{matrix} \right)， \left( \begin{matrix} \displaystyle\frac{15}{48} \ \displaystyle\frac{11}{48} \ \displaystyle\frac{11}{48} \ \displaystyle\frac{11}{48} \end{matrix} \right)， \left( \begin{matrix} \displaystyle\frac{11}{32} \ \displaystyle\frac{7}{32} \ \displaystyle\frac{7}{32} \ \displaystyle\frac{7}{32} \end{matrix} \right)，\cdots， \left( \begin{matrix} \displaystyle\frac{3}{9} \ \displaystyle\frac{2}{9} \ \displaystyle\frac{2}{9} \ \displaystyle\frac{2}{9} \end{matrix} \right)$$
case2:终止点(网页C不指向任何网页)
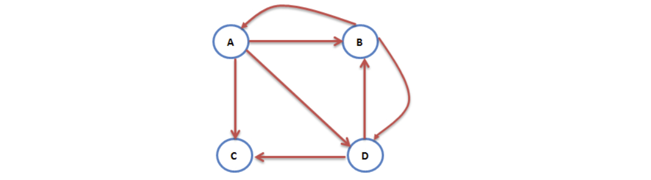
$$T= \left( \begin{matrix} 0 & \displaystyle\frac{1}{2} & 0 & 0\ \displaystyle\frac{1}{3} & 0 & 0 & \displaystyle\frac{1}{2}\ \displaystyle\frac{1}{3} & 0 & 0 & \displaystyle\frac{1}{2}\ \displaystyle\frac{1}{3} & \displaystyle\frac{1}{2} & 0 & 0 \end{matrix} \right)$$
$$\left( \begin{matrix} \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \end{matrix} \right)， \left( \begin{matrix} \displaystyle\frac{3}{24} \ \displaystyle\frac{5}{24} \ \displaystyle\frac{5}{24} \ \displaystyle\frac{5}{24} \end{matrix} \right)， \left( \begin{matrix} \displaystyle\frac{5}{48} \ \displaystyle\frac{7}{48} \ \displaystyle\frac{7}{48} \ \displaystyle\frac{7}{48} \end{matrix} \right)， \left( \begin{matrix} \displaystyle\frac{21}{288} \ \displaystyle\frac{31}{288} \ \displaystyle\frac{31}{288} \ \displaystyle\frac{31}{288} \end{matrix} \right)，\cdots， \left( \begin{matrix} 0 \ 0 \ 0 \ 0 \end{matrix} \right)$$
即上网者达到终止点后，无法确定下一步的走哪。
case3:陷阱点(网页C只指向自身)
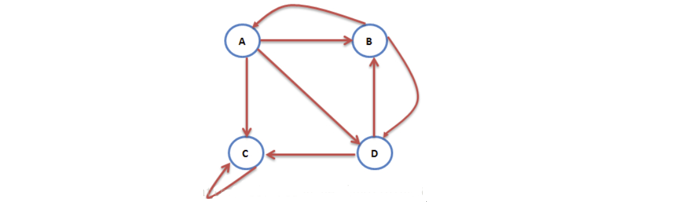$$T= \left( \begin{matrix} 0 & \displaystyle\frac{1}{2} & 0 & 0\ \displaystyle\frac{1}{3} & 0 & 0 & \displaystyle\frac{1}{2}\ \displaystyle\frac{1}{3} & 0 & 1 & \displaystyle\frac{1}{2}\ \displaystyle\frac{1}{3} & \displaystyle\frac{1}{2} & 0 & 0 \end{matrix} \right)$$
$$\left( \begin{matrix} \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \ \displaystyle\frac{1}{4} \end{matrix} \right)， \left( \begin{matrix} \displaystyle\frac{3}{24} \ \displaystyle\frac{5}{24} \ \displaystyle\frac{11}{24} \ \displaystyle\frac{5}{24} \end{matrix} \right)， \left( \begin{matrix} \displaystyle\frac{5}{48} \ \displaystyle\frac{7}{48} \ \displaystyle\frac{29}{48} \ \displaystyle\frac{7}{48} \end{matrix} \right)， \left( \begin{matrix} \displaystyle\frac{21}{288} \ \displaystyle\frac{31}{288} \ \displaystyle\frac{205}{288} \ \displaystyle\frac{31}{288} \end{matrix} \right)，\cdots， \left( \begin{matrix} 0 \ 0 \ 1 \ 0 \end{matrix} \right)$$
即上网者达到陷阱点后，无法从陷阱点出来。
STEP3
通常当上网者走到一个终止点网页或陷阱点网页，他可以在浏览器的地址栏随机输入一个网址(这个网址可能是原来的网页，也可能是别的网页)，这给了该上网者一个逃离的机会。此外，上网者可能在每浏览一个网页时，都有可能不想看当前网页上的链接，而是在地址栏输入一个网址。
假设上网者在浏览器地址栏输入跳转到各个网页的概率是$\displaystyle\frac{1}{N}$，上网者每一步查看当前网页的概率为$\alpha$，则该上网者选择从浏览器地址栏跳转的概率为$1-\alpha$，则迭代公式
$$V_n = \alpha T \cdot V_{n-1} + (1-\alpha) e，其中e= \left( \begin{matrix} \displaystyle\frac{1}{N} \ \displaystyle\frac{1}{N} \ \vdots \ \displaystyle\frac{1}{N} \end{matrix} \right)$$
这里，$\alpha\in[0,1]$通常取值$0.85$，$\alpha$的大小与算法的收敛速度成反比，如果$\alpha$取值过大会导致收敛速度过慢，$\alpha$取值过小就无法体现pagerank算法的作用(前半部分的迭代计算$PR$值)。
算法的不足
（1）没有区分站内导航链接(很多网站的首页都有很多 对站内其他页面的链接)。这些链接与不同网站之间的链接相比，肯定是后者更能体现$PR$值的传递关系。
（2）没有过滤广告链接和功能链接(如常见的“分享到微博”)。前者链接到广告页面，后者常常链接到某个社交网站首页；而这些链接通常没有什么实际价值。
（3）对新网页不友好。一般一个新网页的入链相对较少，即使它的内容的质量很高，要成为一个高PR值的页面仍需要很长时间的推广。
