主要内容:Apriori算法、频繁项集生成、关联规则生成、投票中的关联规则发现
缺点:是在大数据集上可能较慢。
当寻找频繁项集时,有两个概念比较重要:
支持度和
可信度。
| 交易号码 | 商品 |
| 0 | 豆奶, 莴苣 |
| 1 | 莴苣,尿布,葡萄酒,甜菜 |
| 2 | 莴苣,尿布,葡萄酒,橙汁 |
| 3 | 莴苣,豆奶,尿布,葡萄酒 |
| 4 | 莴苣,豆奶,尿布,橙汁 |
1 | 1 |
支持度:一个项集的支持度(support)被定义为数据集中包含该项集的记录占总记录的比例。从表1 可以看出 项集 {豆奶} 的支持度为 4/5; 而在 5 条交易记录中 3 条包含 {豆奶,尿布},因此 {豆奶,尿布} 的支持度为 3/5.
可信度或置信度(confidence):是针对一条诸如尿布−−>葡萄酒尿布−−>葡萄酒的关联规则来定义的,这条规则的可信度被定义为“ 支持度({尿布,葡萄酒}) / 支持度({尿布})”。在表1 中可以发现 {尿布,葡萄酒} 的支持度是 3/53/5, {尿布} 的支持度为 4/54/5, 所以关联规则 “尿布 –> 葡萄酒”的可信度为 3/4=0.753/4=0.75, 意思是对于所有包含 "尿布"的记录中,该关联规则对其中的 75% 记录都适用。
因为网上的代码和原著的代码运行后会报一些错误,所以本文修改了两个地方,将C1和D都强制转换为list类型,程序才能正常运行。
# 构建第一个候选项集列表C1
C1 = list(createC1(myDat))
# 构建集合表示的数据集 D
D = list(map(set, myDat))
apriori.py
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
2def loadDataSet():
3 '''创建一个用于测试的简单的数据集'''
4 return [ [ 1, 3, 4 ], [ 2, 3, 5 ], [ 1, 2, 3, 5 ], [ 2, 5 ] ]
5
6def createC1( dataSet ):
7 '''
8 构建初始候选项集的列表,即所有候选项集只包含一个元素,
9 C1是大小为1的所有候选项集的集合
10 '''
11 C1 = []
12 for transaction in dataSet:
13 for item in transaction:
14 if [ item ] not in C1:
15 C1.append( [ item ] )
16 C1.sort()
17 return map( frozenset, C1 )
18
19def scanD( D, Ck, minSupport ):
20 '''
21 计算Ck中的项集在数据集合D(记录或者transactions)中的支持度,
22 返回满足最小支持度的项集的集合,和所有项集支持度信息的字典。
23 '''
24 ssCnt = {}
25 for tid in D:
26 # 对于每一条transaction
27 for can in Ck:
28 # 对于每一个候选项集can,检查是否是transaction的一部分
29 # 即该候选can是否得到transaction的支持
30 if can.issubset( tid ):
31 ssCnt[can] = ssCnt.get(can, 0) + 1
32 numItems = float(len(D))
33 retList = []
34 supportData = {}
35 for key in ssCnt:
36 # 每个项集的支持度
37 support = ssCnt[ key ] / numItems
38 # 将满足最小支持度的项集,加入retList
39 if support >= minSupport:
40 retList.insert( 0, key )
41 # 汇总支持度数据
42 supportData[ key ] = support
43 return retList, supportData
44
45if __name__ == '__main__':
46 # 导入数据集
47 myDat = loadDataSet()
48 # 构建第一个候选项集列表C1
49 C1 = list(createC1(myDat))
50
51 # 构建集合表示的数据集 D
52 D = list(map(set, myDat))
53
54 # 选择出支持度不小于0.5 的项集作为频繁项集
55 L, suppData = scanD( D, C1, 0.5 )
56
57 print ("频繁项集L:", L)
58 print ("所有候选项集的支持度信息:", suppData)
59
60
输出:
2
3
4
2所有候选项集的支持度信息: {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75}
3
4
可以看出,只有支持度不小于 0.5 的项集被选中到 L 中作为频繁项集,根据不同的需求,我们可以设定最小支持度的值,从而得到我们想要的频繁项集。
上述支队单元素进行了检查,为形成完整的apriori算法:
在上面代码中添加:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
2# Aprior算法
3def aprioriGen( Lk, k ):
4 '''
5 由初始候选项集的集合Lk生成新的生成候选项集,
6 k表示生成的新项集中所含有的元素个数
7 '''
8 retList = []
9 lenLk = len( Lk )
10 for i in range( lenLk ):
11 for j in range( i + 1, lenLk ):
12 L1 = list( Lk[ i ] )[ : k - 2 ];
13 L2 = list( Lk[ j ] )[ : k - 2 ];
14 L1.sort();L2.sort()
15 if L1 == L2:
16 retList.append( Lk[ i ] | Lk[ j ] )
17 return retList
18
19def apriori( dataSet, minSupport = 0.5 ):
20 # 构建初始候选项集C1
21 C1 = list(createC1( dataSet ))
22 # 将dataSet集合化,以满足scanD的格式要求
23 D = list(map( set, dataSet ))
24 # 构建初始的频繁项集,即所有项集只有一个元素
25 L1, suppData = scanD( D, C1, minSupport )
26 L = [ L1 ]
27 # 最初的L1中的每个项集含有一个元素,新生成的
28 # 项集应该含有2个元素,所以 k=2
29 k = 2
30 while ( len( L[ k - 2 ] ) > 0 ):
31 Ck = aprioriGen( L[ k - 2 ], k )
32 Lk, supK = scanD( D, Ck, minSupport )
33 # 将新的项集的支持度数据加入原来的总支持度字典中
34 suppData.update( supK )
35 # 将符合最小支持度要求的项集加入L
36 L.append( Lk )
37 # 新生成的项集中的元素个数应不断增加
38 k += 1
39 # 返回所有满足条件的频繁项集的列表,和所有候选项集的支持度信息
40 return L, suppData
41
42if __name__ == '__main__':
43# # 导入数据集
44# myDat = loadDataSet()
45# # 构建第一个候选项集列表C1
46# C1 = list(createC1(myDat))
47# # 构建集合表示的数据集 D
48# D = list(map(set, myDat))
49# # 选择出支持度不小于0.5 的项集作为频繁项集
50# L, suppData = scanD( D, C1, 0.5 )
51# print ("频繁项集L:", L)
52# print ("所有候选项集的支持度信息:", suppData)
53
54 # 导入数据集
55 myDat = loadDataSet()
56 # 选择频繁项集
57 L, suppData = apriori( myDat, 0.5 )
58 print ("频繁项集L:", L)
59 print ("所有候选项集的支持度信息:", suppData)
60
输出:
2
3
4
2所有候选项集的支持度信息: {frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({1, 3}): 0.5, frozenset({2, 5}): 0.75, frozenset({3, 5}): 0.5, frozenset({2, 3}): 0.5, frozenset({1, 5}): 0.25, frozenset({1, 2}): 0.25, frozenset({2, 3, 5}): 0.5}
3
4
从频繁项集中挖掘关联规则:
要找到关联规则,先从一个频繁集开始,我们想知道对于频繁项集中的元素能否获取其它内容,即某个元素或者某个集合可能会推导出另一个元素。从表1 可以得到,如果有一个频繁项集 {豆奶,莴苣},那么就可能有一条关联规则 "豆奶 –> 莴苣",意味着如果有人购买了豆奶,那么在统计上他会购买莴苣的概率较大。但是这一条反过来并不一定成立。
从一个频繁项集可以产生多少条关联规则呢?可以基于该频繁项集生成一个可能的规则列表,然后测试每条规则的可信度,如果可信度不满足最小值要求,则去掉该规则。类似于前面讨论的频繁项集生成,一个频繁项集可以产生许多可能的关联规则,如果能在计算规则可信度之前就减少规则的数目,就会很好的提高计算效率。
这里有一条规律就是:如果某条规则并不满足最小可信度要求,那么该规则的所有子集也不会满足最小可信度要求,例如下图的解释:
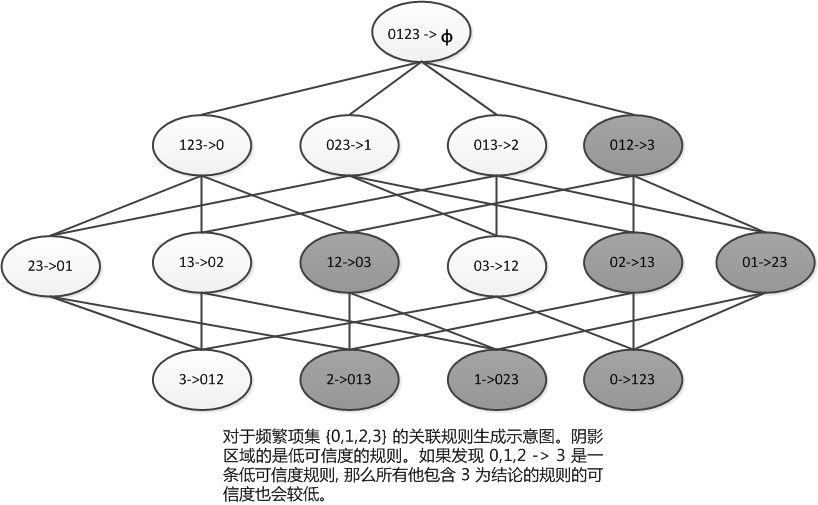
所以,可以利用上图所示的性质来减少测试的规则数目。
关联规则生成函数清单:
在py文件中添加:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
2def calcConf( freqSet, H, supportData, brl, minConf=0.7 ):
3 '''
4 计算规则的可信度,返回满足最小可信度的规则。
5
6 freqSet(frozenset):频繁项集
7 H(frozenset):频繁项集中所有的元素
8 supportData(dic):频繁项集中所有元素的支持度
9 brl(tuple):满足可信度条件的关联规则
10 minConf(float):最小可信度
11 '''
12 prunedH = []
13 for conseq in H:
14 conf = supportData[ freqSet ] / supportData[ freqSet - conseq ]
15 if conf >= minConf:
16 print(freqSet - conseq, '-->', conseq, 'conf:', conf)
17 brl.append( ( freqSet - conseq, conseq, conf ) )
18 prunedH.append( conseq )
19 return prunedH
20
21def rulesFromConseq( freqSet, H, supportData, brl, minConf=0.7 ):
22 '''
23 对频繁项集中元素超过2的项集进行合并。
24
25 freqSet(frozenset):频繁项集
26 H(frozenset):频繁项集中的所有元素,即可以出现在规则右部的元素
27 supportData(dict):所有项集的支持度信息
28 brl(tuple):生成的规则
29
30 '''
31 m = len( H[ 0 ] )
32
33 # 查看频繁项集是否大到移除大小为 m 的子集
34 if len( freqSet ) > m + 1:
35 Hmp1 = aprioriGen( H, m + 1 )
36 Hmp1 = calcConf( freqSet, Hmp1, supportData, brl, minConf )
37
38 # 如果不止一条规则满足要求,进一步递归合并
39 if len( Hmp1 ) > 1:
40 rulesFromConseq( freqSet, Hmp1, supportData, brl, minConf )
41
42def generateRules( L, supportData, minConf=0.7 ):
43 '''
44 根据频繁项集和最小可信度生成规则。
45
46 L(list):存储频繁项集
47 supportData(dict):存储着所有项集(不仅仅是频繁项集)的支持度
48 minConf(float):最小可信度
49 '''
50 bigRuleList = []
51 for i in range( 1, len( L ) ):
52 for freqSet in L[ i ]:
53 # 对于每一个频繁项集的集合freqSet
54 H1 = [ frozenset( [ item ] ) for item in freqSet ]
55
56 # 如果频繁项集中的元素个数大于2,需要进一步合并
57 if i > 1:
58 rulesFromConseq( freqSet, H1, supportData, bigRuleList, minConf )
59 else:
60 calcConf( freqSet, H1, supportData, bigRuleList, minConf )
61 return bigRuleList
62
63if __name__ == '__main__':
64# # 导入数据集
65# myDat = loadDataSet()
66# # 构建第一个候选项集列表C1
67# C1 = list(createC1(myDat))
68# # 构建集合表示的数据集 D
69# D = list(map(set, myDat))
70# # 选择出支持度不小于0.5 的项集作为频繁项集
71# L, suppData = scanD( D, C1, 0.5 )
72# print ("频繁项集L:", L)
73# print ("所有候选项集的支持度信息:", suppData)
74
75
76# # 导入数据集
77# myDat = loadDataSet()
78# # 选择频繁项集
79# L, suppData = apriori( myDat, 0.7 )
80# print ("频繁项集L:", L)
81# print ("所有候选项集的支持度信息:", suppData)
82
83 # 导入数据集
84 myDat = loadDataSet()
85 # 选择频繁项集
86 L, suppData = apriori( myDat, 0.5 ) #调节支持度
87
88 rules = generateRules( L, suppData, minConf=0.7 ) #调节可信度
89 print('rules:\n', rules)
90
输出:
2
3
4
5
6
7
2frozenset({2}) --> frozenset({5}) conf: 1.0
3frozenset({1}) --> frozenset({3}) conf: 1.0
4rules:
5 [(frozenset({5}), frozenset({2}), 1.0), (frozenset({2}), frozenset({5}), 1.0), (frozenset({1}), frozenset({3}), 1.0)]
6
7
一旦降低可信度阈值,就可以获得更多的规则。
有上面分析可以看出 Apriori 算法易编码,缺点是在大数据集上可能较慢。
