《目录》
- 插入排序
- 循环不变式
- 优化插入排序
算法导论的第二章，以一个简单的算法(插入排序)入手，讲解算法分析里一些关键的技术。
算法是计算方法的简称，而计算方法是为了解决问题而存在的。
那么插入排序这样的算法是因为是什么问题而存在的呢 ？
：排序问题。
插入排序
请用数学语言结合算法的要求来描述排序问题，以保证问题的清晰、简洁、直接、齐整。
输入： 个数的一个序列 ；
输出：序列的排列 ，满足 。
我们称排序的数为 key，算法的核心就是为一系列的 key 排序，对这些 key 排序需要用的某种算法。
算法导论举了一个很有意思的例子，拿扑克牌的抓牌形式来类比某种算法。
左手拿的牌，是已经排好顺序的。右手就从牌堆里头取一张牌，取出来后再放在左手中合适的位置。
这种插入算法牌多了，效率就低了，右边的图就表示还有比插入排序更好的方法，不过因为插入排序好理解，我们以插入排序为例。
其次，插入排序运用在小规模问题上，效率还是挺好的。
插入排序的算法步骤：
- 左手为空且桌子上的牌面向下
- 每次从桌子上拿走一张牌并插在合适的位置上
- 为了找到某张牌的正确位置，从右到左将 ta 与已在手中的每张牌进行比较，保证左手拿着的牌都是排序好的
我们已经确定了这种算法，而且已经知道了算法原理(扑克牌排序)。
首先，确定算法的名字以及此算法的函数声明原型。
- 名字：Insertion_sort
- 函数原型：需不需要输入参数(应该传什么参数给函数)、需不需要输出参数(把什么数据作为结果返回)。
分析：
-
排序算法需要有 个数的一个序列，传一个数组 做为输入参数即可；
-
输出的是一个序列，就地排序，不需要申请新的空间，因此，没有输出参数，空间复制度为常数 。
2
3
4
5
2#define T int
3
4void Insertion_sort(T arr[], int len){ ... }
5
接下来，就是算法的边界判断了，为了程序的安全，要对输入参数进行严格的审查。
……
描述插入排序，我们最好先举一例子看看：。
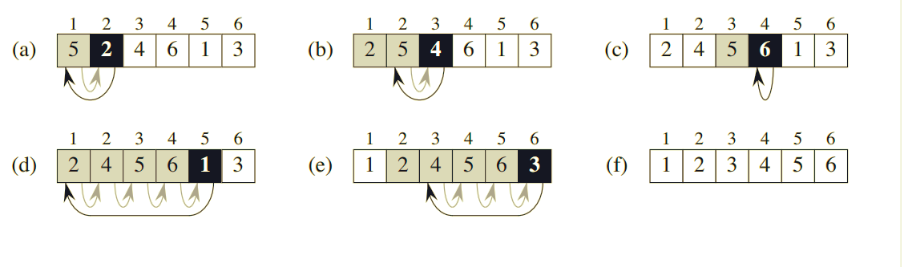
以 图为例，有 灰格、黑格、白格：
- 灰格：左手上已排序好的牌
- 黑格：右手抓的排，需要找到一个合适的位置
- 白格：桌上的牌，目前没什么作用
我来模拟过程：
总结：算法比较简单，每次处理一个新的元素，从后往前(数组)去看，挨个比较找到合适的地方，而后移动即可。
细节：挨个比较需要俩个数组下标或俩个指针，另外，循环开始的时候可以从第 2 个元素开始(因为第 1 个元素位置确定，不需要排序)。
算法实现：
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2for(int i=1; i<ARRAY_SIZE(arr); i++)
3{
4 T key = arr[i]; // arr[i] 这个元素，先抓起来
5
6 int j=i-1; // 从后往前看，下标 = i-1，注意：i最小时下标为1。
7
8 while( key < arr[j] ){ // 抓的牌比左手上的牌小时
9 arr[j+1] = arr[j]; // 找到合适的位置(往后挪动一位)
10
11 /*
12 算法结束条件：
13 1. 牌抓完了 即 j = 0
14 2. 抓的牌大于左手上的牌 即 key > arr[j]
15 */
16 if( (j--) == 0 ) // 从后往前看，即 j--
17 break; // 这一步可以优化，使用短路表达式优化: while( (j--) > 0 && key < arr[j] )
18
19 }
20 arr[j+1] = key; // 位置确定，插入在后面
21}
22
完整版：
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
2
3// 定义通用类型
4#define T int
5
6void Insertion_sort( T arr[], int len){
7for(int i=1; i<len; i++)
8{
9 T key = arr[i];
10
11 int j=i-1; // 从后往前看，下标 = i-1，注意：i最小时下标为1。
12
13 while( key < arr[j] ){ // 抓的牌比左手上的牌小时
14 arr[j+1] = arr[j]; // 寻找合适的位置(往后挪动一位)
15
16 /*
17 算法结束条件：
18 1. 牌抓完了 即 j = 0
19 2. 抓的牌大于左手上的牌 即 key > arr[j]
20 */
21 if( (j--) == 0 ) // 从后往前看，即 j--
22 break;
23
24 }
25 arr[j+1] = key; // 位置确定，插入到后面
26}
27}
28
29int main( )
30{
31 T a[] = {5, 2, 4, 6, 1, 3};
32 int len = sizeof(a)/sizeof(a[0]);
33 Insertion_sort(a, len);
34 for( int i=0; i<len; i++ )
35 printf("%d ", a[i]);
36}
37
插入排序的运行时间在渐进意义上是较菜的，我们主要的目的是通过插入排序，讲解算法分析里一些关键的技术，比如：循环不变式。
循环不变式
循环不变式可以理解为循环中不可不遵循的一个规则。
举个例子，只能一对一的线性表就是个数据结构不变式(为了保证性能，结构上的特性必须满足)。
在插入排序中，从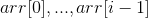 
的元素已排序，这就是一个循环不变式。
没有排序的部分，从 的元素，是一个向未处理的一个序列。
整个插入排序就是把没有排序的部分排序，这个过程和数学归纳法类似。
- 有一个基础情形，排序刚开始只有一个元素，没有顺序；
- 假设推进，从
的元素已排序，此时再加一个新的元素进去，仍然排完序； - 所以，到最后一个元素也是排好顺序的。
处理循环不变式的过程：
- 初始化：循环的第一次迭代之前，ta 为真： 有序。
- 维护不变式：如果循环的某次迭代之前 ta 为真，那下次迭代之前 ta 仍为真： 有序， 也有序。
- 终结： 有序，排序完成。
具体的证明，建议参考《算法导论》。
优化插入排序
上面的插入排序，是从后往前查找，这种查找就是顺序查找。
如果要做优化，我们完全可以用二分查找代替顺序查找。
思想是这样，其实也不用我们自己写：C++ 的模版库里有 lower_bound() 可用，TA 的时间复杂度为 。
我封装在下面了：数组、查找方法都用模版库的，很酷很酷的。
2
3
4
5
6
7
8
9
10
11
12
13
2void insertion_sort(std::vector<T>& V)
3{
4 for (size_t i = 1; i < V.size(); ++i)
5 {
6 auto key = V[i];
7 auto position = std::lower_bound(V.begin(), V.begin() + i, key);
8 for (auto iter = V.begin() + i; iter > position; --iter)
9 *iter = *(iter - 1);
10 *position = key;
11 }
12}
13
C++ 版测试性能 90万个数，可以开到上亿试一试，单位是 min。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
2#include <vector>
3#include <algorithm>
4#include <random>
5#include <ctime>
6
7template <typename T>
8void insertion_sort(std::vector<T>& V)
9{
10 for (size_t i = 1; i < V.size(); ++i)
11 {
12 auto key = V[i];
13 auto position = std::lower_bound(V.begin(), V.begin() + i, key);
14 for (auto iter = V.begin() + i; iter > position; --iter)
15 *iter = *(iter - 1);
16 *position = key;
17 }
18}
19
20int main()
21{
22 double start_t, end_t; // 计时器.
23
24 // 内存分配计时开始.
25 start_t = clock();
26 std::vector<double> V(900000); // 90万个数, 需要6.9MB内存.
27 // 内存分配计时结束并输出时间.
28 end_t = clock();
29 std::cout << (end_t - start_t) / (CLOCKS_PER_SEC * 60)
30 << " minutes" << std::endl;
31
32 // 数据赋值计时开始.
33 start_t = clock();
34 // 利用随机数生成器生成0.0到1.0之间的实数.
35 std::default_random_engine generator(time(NULL));
36 std::uniform_real_distribution<double> distribution(0.0, 1.0);
37 for (size_t i = 0; i < V.size(); ++i)
38 V[i] = distribution(generator);
39 // 数据赋值计时结束并输出时间.
40 end_t = clock();
41 std::cout << (end_t - start_t) / (CLOCKS_PER_SEC * 60)
42 << " minutes" << std::endl;
43
44 // 排序计时开始.
45 start_t = clock();
46 // 插入排序相当慢.
47 insertion_sort(V);
48 // 排序计时结束并输出时间.
49 end_t = clock();
50 std::cout << (end_t - start_t) / (CLOCKS_PER_SEC * 60)
51 << " minutes" << std::endl;
52
53 return 0;
54}
55
