这个算法主要要弄懂三个循环的顺序关系。
弗洛伊德(Floyd)算法过程:
1、用D[v][w]记录每一对顶点的最短距离。
2、依次扫描每一个点,并以其为基点再遍历所有每一对顶点D[][]的值,看看是否可用过该基点让这对顶点间的距离更小。
算法理解:
最短距离有三种情况:
1、两点的直达距离最短。(如下图<v,x>)
2、两点间只通过一个中间点而距离最短。(图<v,u>)
3、两点间用通过两各以上的顶点而距离最短。(图<v,w>)
对于第一种情况:在初始化的时候就已经找出来了且以后也不会更改到。
对于第二种情况:弗洛伊德算法的基本操作就是对于每一对顶点,遍历所有其它顶点,看看可否通过这一个顶点让这对顶点距离更短,也就是遍历了图中所有的三角形(算法中对同一个三角形扫描了九次,原则上只用扫描三次即可,但要加入判断,效率更低)。
对于第三种情况:如下图的五边形,可先找一点(比如x,使<v,u>=2),就变成了四边形问题,再找一点(比如y,使<u,w>=2),可变成三角形问题了(v,u,w),也就变成第二种情况了,由此对于n边形也可以一步步转化成四边形三角形问题。(这里面不用担心哪个点要先找哪个点要后找,因为找了任一个点都可以使其变成(n-1)边形的问题)。
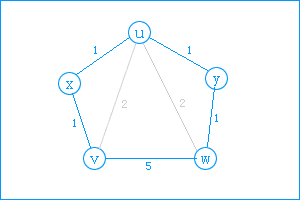
结合代码 并参照上图所示 我们来模拟执行下 这样才能加深理解:
第一关键步骤:当k执行到x,i=v,j=u时,计算出v到u的最短路径要通过x,此时v、u联通了。
第二关键步骤:当k执行到u,i=v,j=y,此时计算出v到y的最短路径的最短路径为v到u,再到y(此时v到u的最短路径上一步我们已经计算过来,直接利用上步结果)。
第三关键步骤:当k执行到y时,i=v,j=w,此时计算出最短路径为v到y(此时v到y的最短路径长在第二步我们已经计算出来了),再从y到w。
依次扫描每一点(k),并以该点作为中介点,计算出通过k点的其他任意两点(i,j)的最短距离,这就是floyd算法的精髓!同时也解释了为什么k点这个中介点要放在最外层循环的原因.
对于这个算法,网上有一个证明的版本:
floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在),floyd算法加入了这个概念 A
k(i,j):表示从i到j
中途不经过索引比k大的点的最短路径。
这个限制的重要之处在于,它将最短路径的概念做了限制,使得该限制有机会满足迭代关系,这个迭代关系就在于研究:假设A
k(i,j)已知,是否可以借此推导出A
k-1(i,j)。
假设我现在要得到A
k(i,j),而此时A
k(i,j)已知,那么我可以分两种情况来看待问题:1. A
k(i,j)沿途经过点k;2. A
k(i,j)不经过点k。如果经过点k,那么很显然,A
k(i,j) = A
k-1(i,k) + A
k-1(k,j),为什么是A
k-1呢?因为对(i,k)和(k,j),由于k本身就是源点(或者说终点),加上我们求的是A
k(i,j),所以满足不经过比k大的点的条件限制,且已经不会经过点k,故得出了A
k-1这个值。那么遇到第二种情况,A
k(i,j)不经过点k时,由于没有经过点k,所以根据概念,可以得出A
k(i,j)=A
k-1(i,j)。现在,我们确信有且只有这两种情况—不是经过点k,就是不经过点k,没有第三种情况了,条件很完整,那么是选择哪一个呢?很简单,求的是最短路径,当然是哪个最短,求取哪个,故得出式子:
A
k(i,j) = min( A
k-1(i,j), A
k-1(i,k) + A
k-1(k,j) )
现在已经得出了A
k(i,j) = A
k-1(i,k) + A
k-1(k,j)这个递归式,但显然该递归还没有一个出口,也就是说,必须定义一个初始状态,事实上,这个初始状态取决于索引k是从0开始还是从1开始,上面的代码是C写的,是以0为开始索引,但一般描述算法似乎习惯用1做开始索引,如果是以1为开始索引,那么初始状态值应设置为A
0了,A
0(i,j)的含义不难理解,即从i到j的边的距离。也就是说,A
0(i,j) = cost(i,j) 。由于存在i到j不存在边的情况,也就是说,在这种情况下,cost(i,j)无限大,故A
0(i,j) = oo(当i到j无边时)
到这里,已经列出了求取A
k(i,j)的整个算法了,但是,最终的目标是求dist(i,j),即i到j的最短路径,如何把A
k(i,j)转换为dist(i,j)?这个其实很简单,当k=n(n表示索引的个数)的时候,即是说,A
n(i,j)=dist(i,j)。那是因为当k已经最大时,已经不存在索引比k大的点了,那这时候的A
n(i,j)其实就已经是i到j的最短路径了。
从floyd算法中不难看出,要设计一个好的动态规划算法,首先需要研究是否能把目标进行重新诠释(这一步是最关键最富创造力的一步),转化为一个可以被分解的子目标,如果可以转化,就要想办法寻找数学等式使目标收敛为子目标,如果这一步可以实现了,还需要研究该递归收敛式的出口,即初始状态是否明确(这一步往往已经简单了)。
如果需要保存最短路径,需要借助path数组:
其中我们用 path 数组记录 经过路径 其实 path 的定义如下 path[i][j] = k 表示 是最短路径 i-……j 和 j 的直接 前驱 为 k 即是: i–>……………–>k ->j
举例子:
如 1-> 5->4 4->3->6 此时 path[1][6] = 0 ; 0表示 1->6 不通 当我们 引入 节点 k = 4 此时有 1->5->4->3->6 显然有 paht[1][6] = 3 = paht[4][6] = paht[k][6]
于是有 path[i][j] = path[k][j]
对于 1->5 相邻边 我们可以在初始化时候 有 paht[1][5] = 1;
如是对于 最短路径 1->5->4->3->6 有 paht[1][6] = 3; paht[1][3]= 4; paht[1][4] = 5; paht[1][5] =1 如此逆推不难得到 最短路径记录值 。
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
2#include "vector"
3#include "stack"
4#include "fstream"
5using namespace std;
6std::vector<vector<int> > weight;
7std::vector<vector<int> > path;
8int vertexnum;
9int edgenum;
10const int intmax = 10000;
11void initialvector(){
12 weight.resize(vertexnum);//路径权重数组
13 path.resize(vertexnum);//保存最短路径数组,记录前继
14 for(int i = 0;i < vertexnum;i++){//建立数组
15 weight[i].resize(vertexnum,intmax);
16 path[i].resize(vertexnum,-1);
17 }
18}
19void getData(){//获取数据
20 ifstream in("data");
21 in>>vertexnum>>edgenum;
22 initialvector();
23 int from,to;
24 double w;
25 while(in>>from>>to>>w){
26 weight[from][to] = w;
27 path[from][to] = from;//to的前继是from
28 weight[from][from] = 0;//自身到自身的权重为0
29 path[from][from] = from;
30 weight[to][to] = 0;
31 path[to][to] = to;
32 }
33}
34void floyd(){
35 for(int k = 0;k < vertexnum;k++)
36 for(int i= 0;i < vertexnum;i++)
37 for(int j = 0;j < vertexnum;j++){
38 if((weight[i][k] > 0 && weight[k][j] && weight[i][k] < intmax && weight[k][j] < intmax) && (weight[i][k] + weight[k][j] < weight[i][j])){//前面一部分是防止加法溢出
39 weight[i][j] = weight[i][k] + weight[k][j];
40 path[i][j] = path[k][j];
41 }
42 }
43}
44void displaypath(int source,int dest){
45 stack<int> shortpath;
46 int temp = dest;
47 while(temp != source){
48 shortpath.push(temp);
49 temp = path[source][temp];
50 }
51 shortpath.push(source);
52 cout<<"short distance:"<<weight[source][dest]<<endl<<"path:";
53 while(!shortpath.empty()){
54 cout<<shortpath.top()<<" ";
55 shortpath.pop();
56 }
57}
58int main(int argc, char const *argv[])
59{
60 getData();
61 for(int i = 0;i < vertexnum;i++){
62 for(int j = 0;j < vertexnum;j++){
63 cout<<weight[i][j]<<"\t";
64 }
65 cout<<endl;
66 }
67 floyd();
68 displaypath(2,1);
69 return 0;
70}
71
72
数据:
6 9
0 1 3
0 3 4
0 5 5
1 2 1
1 5 5
2 3 5
3 1 3
4 3 3
4 5 2
5 3 2
