洗牌算法
- 导语
- 抽牌 – Fisher-Yates Shuffle
- 换牌 – Knuth-Durstenfeld Shuffle
- 插牌 – Inside-Out Algorithm
- 扩展 – 蓄水池抽样
导语
在之前的【Leetcode 384】Shuffle an Array – MEDIUM,打乱一个数组的问题中,我们有用到洗牌算法,其关键在于生成等概率的结果。
而联系实际的洗牌过程,都有哪几种方式呢?
- 每次随机抽出一张牌 放到一边(不放回),这是抽牌;
- 每次随机抽出一张未处理的牌与当前最后一张牌交换,然后将当前最后一张牌放到一边(不放回),这是换牌;
- 每次随机抽出前 i 张(含第 i 张)中任意一张与第 i 张交换,相当于第 i 张插入到前 i 张中,这是插牌。
抽牌 – Fisher-Yates Shuffle
每次随机抽出一张牌 放到一边(不放回)。
随机性:
元素m被放入第i个位置的概率P = 前i-1个位置选择元素时没有选中m的概率 * 第i个位置选中m的概率。
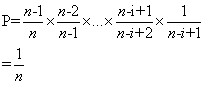
算法实现:
2
3
4
5
6
7
8
9
10
11
12
13
2 Random random = new Random();
3 LinkedList <Integer> temp = new LinkedList<>(list);
4 int index;
5 for(int i=len-1;i>=0;i--){
6 index = random.nextInt(i+1);
7 shuffledNums[i] = initNums[temp.get(index)];
8 temp.remove(index);
9 }
10 return shuffledNums;
11 }
12
13
时间复杂度:O(n)
空间复杂度:O(n)
换牌 – Knuth-Durstenfeld Shuffle
每次随机抽出一张未处理的牌与当前最后一张牌交换,然后将当前最后一张牌放到一边(不放回)。
随机性:
对于任意元素,洗牌后在倒数第 1 个的位置的概率为 1/n(第一次即被选中),倒数第 2 个的位置的概率为[(n-1) / n][ 1 / (n-1)](第一次未被选中,第二次被选中),倒数第 i 个的位置的概率是[(n-1) / n] * [(n-2) / (n-1)] * … * [(n – i + 1) / (n – i + 2)] *[1 / (n – i + 1)] = 1/n。
即任意元素在任意位置的概率均为1 / n。
2
3
4
5
6
7
8
9
10
11
2 Random random = new Random();
3 int index;
4 for(int i=len-1;i>=0;i--){
5 index = random.nextInt(i+1);
6 swap(shuffledNums, index, i);
7 }
8 return shuffledNums;
9 }
10
11
时间复杂度:O(n)
空间复杂度:O(1)
换牌算法与抽牌算法类似,只是没有开辟新的内存空间,而是在原数组内打乱。如果需要保存原序列,仍然需要开辟一个新数组保存下来。
另外,由于它是由后往前遍历的,所以只能针对长度固定且已知的数组打乱。
插牌 – Inside-Out Algorithm
每次随机抽出前 i 张(含第 i 张)中任意一张与第 i 张交换。
随机性:
对于新数组中第 i 个元素,一定是第 i 次被换到了该位置,所以前i – 1次交换的结果与它无关,而它第 i 次被交换至此的概率为1/i,剩余次数内不被暗中的概率为 [ i / (i+1)] * [(i+1) / (i+2)] * [(i+2) / (i+3)]* … * [(n-1) / n ],
所以任意元素在第 i 个位置的概率为1 / n。
算法实现:
2
3
4
5
6
7
8
9
10
11
2 Random random = new Random();
3 int index;
4 for(int i=0;i<len;i++){
5 index = random.nextInt(i+1);
6 swap(shuffledNums, index, i);
7 }
8 return shuffledNums;
9 }
10
11
时间复杂度:O(n)
空间复杂度:O(1)
可以应对长度未知或者长度动态增加的数组打乱问题。
扩展 – 蓄水池抽样
蓄水池是这样一个问题:
给定一个数据流,数据流长度N很大,且N直到处理完所有数据之前都不可知,请问如何在只遍历一遍数据(O(N))的情况下,能够随机选取出m个不重复的数据。
我们可以想象有一个蓄水池,里面包含m个初始元素。
从第k个(m + 1 < = k < = n)开始遍历,从前m+1个元素中随机选取一个元素,如果该元素在蓄水池中,则将其换成当前元素,否则do nothing。
2
3
4
5
6
7
8
9
10
11
12
13
2 Random random = new Random();
3 int[] reservoir = Arrays.copyOf(dataStream, m);
4 int index;
5 for(int i=m; i<dataStream.length;i++){
6 index = random.nextInt(i+1);
7 if(index < m)
8 reservoir[index] = dataStream[i];
9 }
10 return reservoir;
11 }
12
13
时间复杂度:O(n)
空间复杂度:O(m)
