深度学习中的激活函数

Understanding Activation Functions in Deep Learning

激活函数的类型

线性激活函数：这是一种简单的线性函数，公式为：f(x) = x。基本上，输入到输出过程中不经过修改。

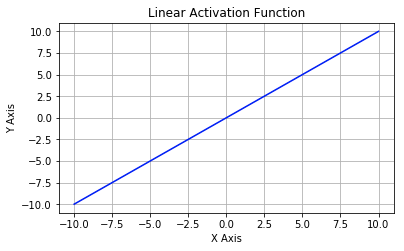
非线性激活函数：用于分离非线性可分的数据，是最常用的激活函数。非线性方程控制输入到输出的映射。非线性激活函数有 Sigmoid、Tanh、ReLU、LReLU、PReLU、Swish 等。下文中将详细介绍这些激活函数。

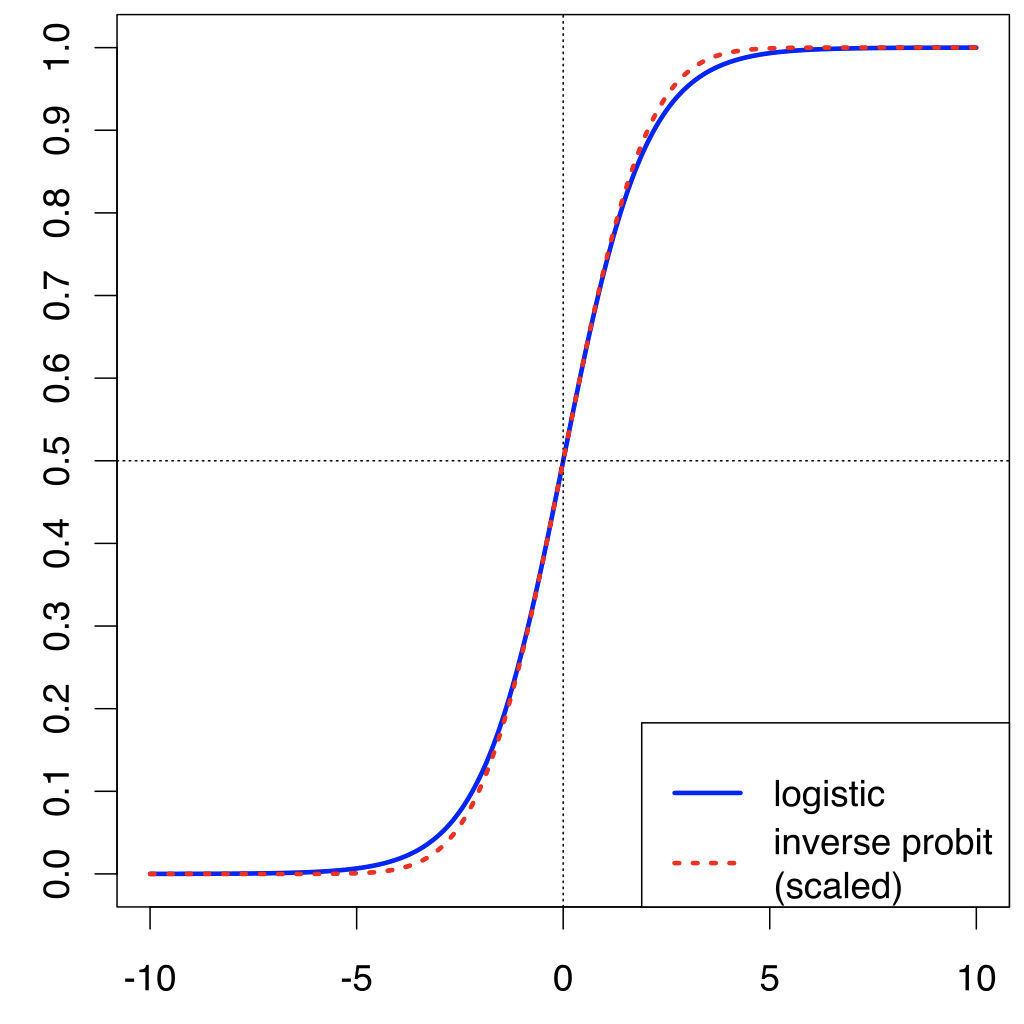
不同类型的非线性激活函数

Sigmoid

Sigmoid又叫作 Logistic 激活函数，它将实数值压缩进 0 到 1 的区间内，还可以在预测概率的输出层中使用。该函数将大的负数转换成 0，将大的正数转换成 1。数学公式为：
$$\sigma(x)=\frac{1}{1 + e^{-x}}$$
下图展示了 Sigmoid 函数及其导数：


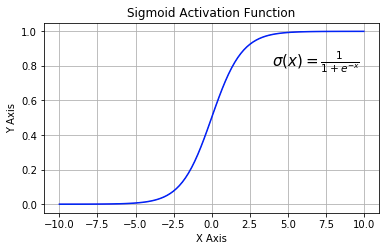
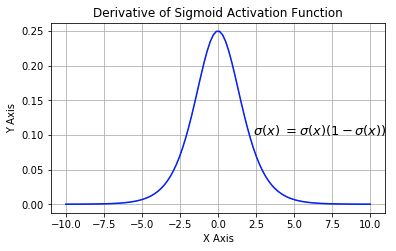
Sigmoid 函数的三个主要缺陷：

1. 梯度消失：注意：Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦，也就是说，Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时，输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此，这些神经元的权重不会更新。此外，与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此，想象一下，如果一个大型神经网络包含 Sigmoid 神经元，而其中很多个都处于饱和状态，那么该网络无法执行反向传播。
2. 不以零为中心：Sigmoid 输出不以零为中心的。
3. 计算成本高昂：exp() 函数与其他非线性激活函数相比，计算成本高昂。

下一个要讨论的非线性激活函数解决了 Sigmoid 函数中值域期望不为 0 的问题。

Tanh

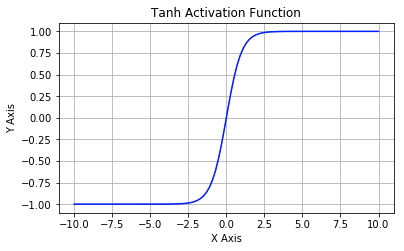
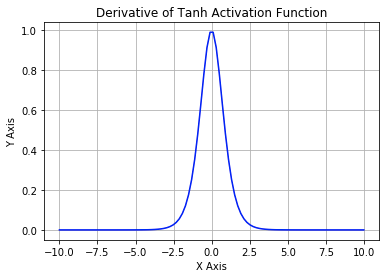
Tanh 激活函数又叫作双曲正切激活函数（hyperbolic tangent activation function）。与 Sigmoid 函数类似，Tanh 函数也使用真值，但 Tanh 函数将其压缩至-1 到 1 的区间内。与 Sigmoid 不同，Tanh 函数的输出以零为中心，因为区间在-1 到 1 之间。你可以将 Tanh 函数想象成两个 Sigmoid 函数放在一起。在实践中，Tanh 函数的使用优先性高于 Sigmoid 函数。负数输入被当作负值，零输入值的映射接近零，正数输入被当作正值。唯一的缺点是：

1. Tanh 函数也会有梯度消失的问题，因此在饱和时也会「杀死」梯度。

为了解决梯度消失问题，我们来讨论另一个非线性激活函数——修正线性单元（rectified linear unit，ReLU），该函数明显优于前面两个函数，是现在使用最广泛的函数。

修正线性单元（ReLU）

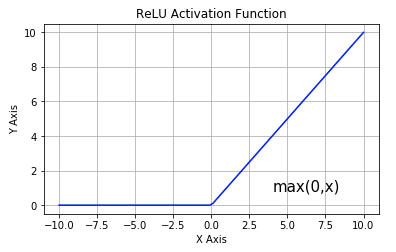
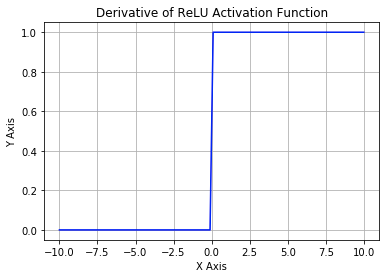
从上图可以看到，ReLU 是从底部开始半修正的一种函数。数学公式为：
$$f(x) = \max(0, x)$$
当输入 $x<0$ 时，输出为 0，当 $x>0$ 时，输出为 x。该激活函数使网络更快速地收敛。它不会饱和，即它可以对抗梯度消失问题，至少在正区域（$x>0$ 时）可以这样，因此神经元至少在一半区域中不会把所有零进行反向传播。由于使用了简单的阈值化（thresholding），ReLU 计算效率很高。但是 ReLU 神经元也存在一些缺点：

1. 不以零为中心：和 Sigmoid 激活函数类似，ReLU 函数的输出不以零为中心。
2. 前向传导（forward pass）过程中，如果 $x<0$，则神经元保持非激活状态，且在后向传导（backward pass）中「杀死」梯度。这样权重无法得到更新，网络无法学习。当 $x=0$ 时，该点的梯度未定义，但是这个问题在实现中得到了解决，通过采用左侧或右侧的梯度的方式。

为了解决 ReLU 激活函数中的梯度消失问题，当 $x<0$ 时，我们使用 Leaky ReLU——该函数试图修复 dead ReLU 问题。下面我们就来详细了解 Leaky ReLU。

Leaky ReLU

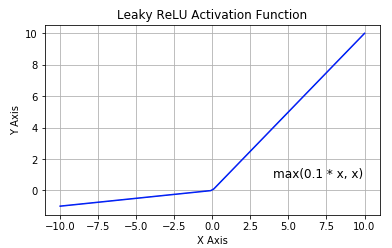
该函数试图缓解 dead ReLU 问题。数学公式为：
$$f(x) = \max(0.1x, x)$$
Leaky ReLU 的概念是：当 $x<0$ 时，它得到 0.1 的正梯度。该函数一定程度上缓解了 dead ReLU 问题，但是使用该函数的结果并不连贯。尽管它具备 ReLU 激活函数的所有特征，如计算高效、快速收敛、在正区域内不会饱和。

Leaky ReLU 可以得到更多扩展。不让 x 乘常数项，而是让 x 乘超参数，这看起来比 Leaky ReLU 效果要好。该扩展就是 Parametric ReLU。

Parametric ReLU

PReLU 函数的数学公式为：
$$f(x) = \max(\alpha x,x)$$
其中$\alpha$是超参数。这里引入了一个随机的超参数$\alpha$，它可以被学习，因为你可以对它进行反向传播。这使神经元能够选择负区域最好的梯度，有了这种能力，它们可以变成 ReLU 或 Leaky ReLU。

总之，最好使用 ReLU，但是你可以使用 Leaky ReLU 或 Parametric ReLU 实验一下，看看它们是否更适合你的问题。

Swish

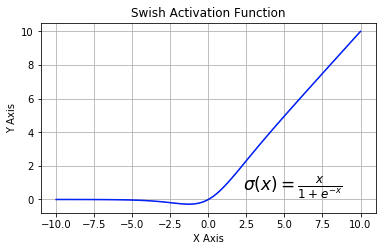
该函数又叫作自门控激活函数，它近期由谷歌的研究者发布，数学公式为：
$$\sigma(x) = \frac{x}{1+e^{-x}}$$
根据论文（https://arxiv.org/abs/1710.05941v1），Swish 激活函数的性能优于 ReLU 函数。

根据上图，我们可以观察到在 x 轴的负区域曲线的形状与 ReLU 激活函数不同，因此，Swish 激活函数的输出可能下降，即使在输入值增大的情况下。大多数激活函数是单调的，即输入值增大的情况下，输出值不可能下降。而 Swish 函数为 0 时具备单侧有界（one-sided boundedness）的特性，它是平滑、非单调的。更改一行代码再来查看它的性能，似乎也挺有意思。