A*算法

1、概论

游戏地图中的路径搜索是人工智能领域中理论在游戏中的一个实际应用，游戏地图的寻路是虚拟角色硬要具备的最基本的能力之一。从虚拟角色的行走可以看出该款游戏的品质，因此寻路成为游戏开发中的重要内容之一。再加上现在的游戏玩家对游戏品质要求越来越高，要求游戏更加真实和逼真，这样对寻路算法就提出了更高的要求。寻路就是角色花费最短的时间以一条最佳的方式走到指定的地点。然而，在游戏地图中寻找路径问题并不仅仅是从起点找到终点的通路那么简单。在游戏中需要考虑很多方面的因素：

• 游戏地图数据量很大，需要很大的存储空间
• 游戏题图非常的复杂，包含很多建筑、草地、河流
• 尽量要和玩家的思考的方式一致

一个好的寻路算法需要满足下面的三个条件：

• 可靠

        在游戏中存在多种地形，只要涉及到自动寻路功能都需要反复调用寻路模块，所以只要起点到终点存在一条通路，算法必须能够保证能够找到该路径。        

• 高效

        算法的时间复杂度不能够影响玩家的感知，如果使用起来存在大量延迟，很多玩家是无法接受的。

• 逼真

        游戏本身就是对真实生活的模拟，对人物的形态，运动的姿态都需要逼真，让玩家有一种身临其境的感觉。

在寻路算法中游戏领域使用最多是是A*算法，本文重点介绍A*算法。在A*算法之前我们先把图的BFS、DFS、弗洛伊德算法、地杰斯特拉算法简单的介绍一下，然后把A*算法说一下，五种算法对比，很容易就能理解A*算法的原理以及区别。

2、地图模拟

以下算法地图生成均使用同样的地图生成器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
1/**

2 * 图

3 *

4 * @author yufei.liu

5 */

6public class Graph {

7

8    /**

9     * 地图

10     */

11    private int[][] map;

12

13    /**

14     * 随机生成一张地图

15     *

16     * @param rowN 行数

17     * @param colN 列数

18     */

19    public Graph createMap(int rowN, int colN) {

20        map = new int[rowN][colN];

21        int obstacleCount = (int) (rowN * colN * 0.05);

22        Random random = new Random();

23        for (int k = 0; k < obstacleCount; k++) {

24            int weight = random.nextInt(4);

25            int height = random.nextInt(4);

26            int startX = (int) (rowN * Math.random());

27            int startY = (int) (colN * Math.random());

28            for (int i = startX; i <= startX + height; i++) {

29                if (i >= rowN) {

30                    continue;

31                }

32                for (int j = startY; j <= startY + weight; j++) {

33                    if (j >= colN) {

34                        continue;

35                    }

36                    map[i][j] = 1;

37                }

38            }

39        }

40        return this;

41    }

42

43}

44

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 

20 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 

30 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 

40 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 

50 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 

60 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 

70 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 0 0 0 

80 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 0 0 0 

90 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 1 

100 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 1 

110 1 1 1 0 1 0 0 0 0 1 1 1 1 1 0 0 0 0 1 

120 1 1 1 0 1 0 0 0 0 1 1 1 1 0 0 0 0 0 0 

130 1 1 1 1 1 1 0 0 0 0 0 1 1 0 0 0 1 1 0 

140 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 

150 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 

160 0 1 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 1 1 

170 0 1 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 1 

180 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 

190 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 

200 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0

21

22@ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ @ 0 

230 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 @ 

240 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 @ 

250 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 @ 

260 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 @ 1 

270 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 @ 1 

280 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 0 0 @ 

290 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 0 0 @ 

300 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 @ 1 

310 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 @ 1 

320 1 1 1 0 1 0 0 0 0 1 1 1 1 1 0 0 0 @ 1 

330 1 1 1 0 1 0 0 0 0 1 1 1 1 0 0 0 @ 0 0 

340 1 1 1 1 1 1 0 0 0 0 0 1 1 0 0 @ 1 1 0 

350 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 @ 1 1 0 

360 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 @ 1 1 1 

370 0 1 0 0 0 0 0 0 0 1 1 1 1 0 0 @ 1 1 1 

380 0 1 0 0 0 0 1 1 1 1 1 1 1 0 0 0 @ @ 1 

390 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 @ 

400 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 @ 

410 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 @ 

42

其中0表示空地，1表示障碍物，@表示一条可行的通路。

3、地图和图的转换

在图中只有结点和边两个概念，边分为有向边和无向边，在地图中有一个一个小格子构成，每一个格子对应图中的一个结点，结点与结点之间的边，在地图上只有“上下左右”（如果允许斜着走也包括左上、右上、左下、右下），在本文中允许斜着走。

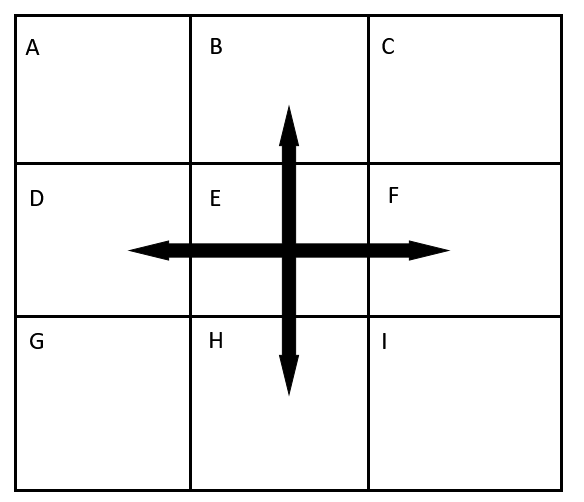
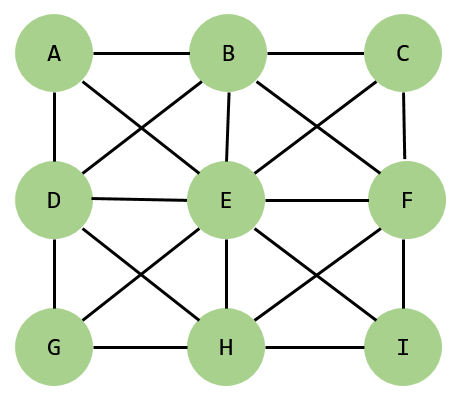
地图到图的转换就和上图展示，注意：

1. 地图非障碍物节点数等于图中的结点数，如果一个20*20的地图，其中障碍物有180个格子，那么转化成图的结点数只有20个。障碍物是不会出现在图上的，障碍物的作用仅仅在于图不是全连接的。
2. 一般来讲，地图生成的图都是无向图，但是一些特殊情形也有可能是有向图，最直接的例子就是单行道。
3. 斜着走和直上直下走对应在图中的区别是边的权重不同，一般情况下，斜边的代价是一个小格子的1.414倍。

4、深度优先、广度优先算法

广度优先算法和深度优先算法本质上都是对图的遍历，算法的目的是从图中的一个节点出发搜索连通的节点节点，并且需要保证不重不漏。遍历结束之后一般我们会关心图的深度、连通性这些基本问题。

在遍历的时候我们可以记录节点的父节点，当遍历到指定节点时，反向查找便可以将整条路径得到。

广度优先和深度优先在设计时稍有不同，深度优先一般使用递归写法，但是从本质上讲广度优先的写法更具有普遍性，所以我们需要将深度优先稍加改造，适配广度优先写法。

首先介绍广度优先：

• 广度优先包含两个表：open表、close表，其中open表存放着待搜索结点列表，close表存放着已经搜索过的结点信息
• 最初open表和close表均为空，将起始结点放入open表
• 不断的从open表取出表头结点，放入close表，并将表头结点的子结点顺序放入open表尾
• 再放入close表检查是否是目标结点。如果是。直接退出
• 当open表为空，直接退出，此时没有找到目标结点，说明目标不可达

对于下面这张图：

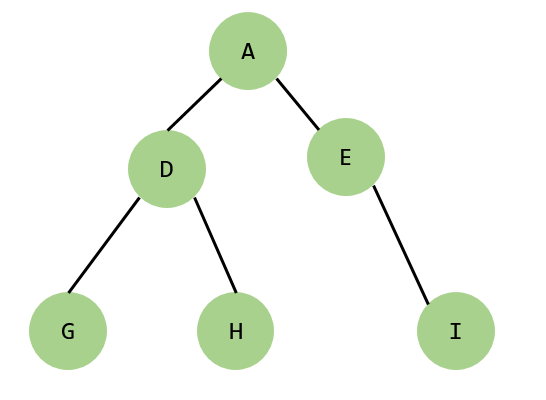
我们很容易可以得到广度优先的序列：ADEGHI

深度优先每一次都访问的是最近的对象。所以深度优先的流程：

• 深度优先包含两个表：open表、close表，其中open表存放着待搜索结点列表，close表存放着已经搜索过的结点信息
• 最初open表和close表均为空，将起始结点放入open表
• 不断的从open表取出表头结点，放入close表，并将表头结点的子结点逆序，并依次插入open表表头
• 再放入close表检查是否是目标结点。如果是。直接退出
• 当open表为空，直接退出，此时没有找到目标结点，说明目标不可达

所以open表中：

A

DE      ————————–> A

GHE   ————————–> D

HE      ————————–> G

E         ————————–> H

I           ————————–> E

            ————————–> I

列一下代码（https://coding.net/u/yfLiu/p/A-star/git/blob/master/src/main/java/com/lyf/csdn/graph/bdfs/BDFS.java）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
1/**

2 * bfs-dfs算法

3 * 这里实现的dfs是一个非递归版本，和bfs算法保持一致

4 *

5 * @author yufei.liu

6 */

7public class BDFS {

8

9    public static final String BFS = "BFS";

10

11    public static final String DFS = "DFS";

12

13    private Graph graph;

14

15    private Point startPoint;

16

17    private Point endPoint;

18

19    public BDFS(Graph graph, Point startPoint, Point endPoint) {

20        this.graph = graph;

21        this.startPoint = startPoint;

22        this.endPoint = endPoint;

23    }

24

25    /**

26     * 深度优先或者广度优先

27     *

28     * @param type  bfs/dfs

29     */

30    public void bdfs(String type) {

31        LinkedList<Point> open = new LinkedList<>();

32        LinkedList<Point> close = new LinkedList<>();

33        Set<Point> openPointSet = new HashSet<>();

34        Set<Point> closePointSet = new HashSet<>();

35

36        Point target = null;

37

38        open.addLast(startPoint);

39        openPointSet.add(startPoint);

40        while (true) {

41            if (open.isEmpty()) {

42                break;

43            }

44            Point point = open.removeFirst();

45            openPointSet.remove(point);

46            close.add(point);

47            closePointSet.add(point);

48

49            if (point.equals(endPoint)) {

50                target = point;

51                break;

52            }

53

54            List<Point> searchPointList= search(point, openPointSet, closePointSet);

55            if (BFS.equals(type)) {

56                for (Point item : searchPointList) {

57                    open.addLast(item);

58                    openPointSet.add(item);

59                }

60            } else if(DFS.equals(type)) {

61                for (int i = searchPointList.size() - 1; i >= 0 ; i--) {

62                    open.addFirst(searchPointList.get(i));

63                    openPointSet.add(searchPointList.get(i));

64                }

65            } else {

66                throw new Error();

67            }

68        }

69        if (target == null) {

70            System.out.println("target is not reachable.");

71        } else {

72            LinkedList<Point> stack = new LinkedList<>();

73            stack.addLast(target);

74            while (true) {

75                target = target.getParentPoint();

76                if (target == null) {

77                    break;

78                }

79                stack.addFirst(target);

80            }

81            graph.printPath(stack);

82        }

83        System.out.println("\n");

84    }

85

86    /**

87     * 上下左右，以及四个斜边方向搜索

88     *

89     * @param point 点

90     * @return      八个方向的点

91     */

92    private List<Point> search(Point point, Set<Point> openPointSet, Set<Point> closePointSet) {

93        LinkedList<Point> points = new LinkedList<>();

94        for (Point item : point.getAllDirectorPoint()) {

95            if (graph.check(item) && !openPointSet.contains(item) && !closePointSet.contains(item)) {

96                points.addLast(item);

97            }

98        }

99        return points;

100    }

101

102}

103

5、弗洛伊德算法

弗洛伊德算法应该是掌握动态规划的第一个算法，算法伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
1Floyd-Warshall算法的描述如下：

21 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)

32 for each vertex v

43    dist[v][v] ← 0

54 for each edge (u,v)

65    dist[u][v] ← w(u,v)  // the weight of the edge (u,v)

76 for k from 1 to |V|

87    for i from 1 to |V|

98       for j from 1 to |V|

109          if dist[i][j] > dist[i][k] + dist[k][j] 

1110             dist[i][j] ← dist[i][k] + dist[k][j]

1211         end if

13

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
1import com.lyf.csdn.graph.graph.Graph;

2import com.lyf.csdn.graph.graph.Point;

3

4import java.util.ArrayList;

5import java.util.List;

6

7/**

8 * 弗洛伊德算法

9 *

10 * @author yufei.liu

11 */

12public class Floyd {

13

14    private Graph graph;

15

16    private Point startPoint;

17

18    private Point endPoint;

19

20    public Floyd(Graph graph, Point startPoint, Point endPoint) {

21        this.graph = graph;

22        this.startPoint = startPoint;

23        this.endPoint = endPoint;

24    }

25

26    @SuppressWarnings("unchecked")

27    public void work() {

28        int[][] map = graph.getMap();

29        int rowN = map.length;

30        int colN = map[0].length;

31        int n = 0;

32        ArrayList<Point> nodeList = new ArrayList<>();

33        for (int i = 0; i < rowN; i++) {

34            for (int j = 0; j < colN; j++) {

35                if (map[i][j] == 0) {

36                    n++;

37                    nodeList.add(new Point(i, j));

38                }

39            }

40        }

41        double[][] dp = new double[n][n];

42        Object[][] dpPath = new Object[n][n];

43        for (int i = 0; i < n; i++) {

44            for (int j = 0; j < n; j++) {

45                dp[i][j] = distance(nodeList.get(i), nodeList.get(j));

46                dpPath[i][j] = new ArrayList<Point>();

47            }

48        }

49        for (int k = 0; k < n; k++) {

50            for (int i = 0; i < n; i++) {

51                for (int j = 0; j < n; j++) {

52                    if (dp[i][k] >= Integer.MAX_VALUE || dp[k][j] >= Integer.MAX_VALUE) {

53                        continue;

54                    }

55                    double temp = dp[i][k] + dp[k][j];

56                    if (temp < dp[i][j]) {

57                        dp[i][j] = temp;

58                        ArrayList<Point> path = (ArrayList<Point>) dpPath[i][j];

59                        ArrayList<Point> pathItoK = (ArrayList<Point>) dpPath[i][k];

60                        ArrayList<Point> pathKtoJ = (ArrayList<Point>) dpPath[k][j];

61                        path.clear();

62                        path.addAll(pathItoK);

63                        path.add(nodeList.get(k));

64                        path.addAll(pathKtoJ);

65                    }

66                }

67            }

68        }

69

70        int startIndex = 0;

71        int targetIndex = 0;

72        for (int i = 0; i < nodeList.size(); i++) {

73            if (nodeList.get(i).equals(startPoint)) {

74                startIndex = i;

75            }

76            if (nodeList.get(i).equals(endPoint)) {

77                targetIndex = i;

78            }

79        }

80        System.out.println("distance = " + dp[startIndex][targetIndex]);

81        graph.printPath((List<Point>) dpPath[startIndex][targetIndex]);

82    }

83

84    /**

85     * 两点之间的距离

86     *

87     * @param start 开始结点

88     * @param end   结束点

89     * @return 距离

90     */

91    private double distance(Point start, Point end) {

92        if (Math.abs(start.getRow() - end.getRow()) > 1 || Math.abs(start.getCol() - end.getCol()) > 1) {

93            return Integer.MAX_VALUE;

94        }

95        if (Math.abs(start.getRow() - end.getRow()) == 0 || Math.abs(start.getCol() - end.getCol()) == 0) {

96            return 1;

97        }

98        return 1.414;

99    }

100

101}

102

103

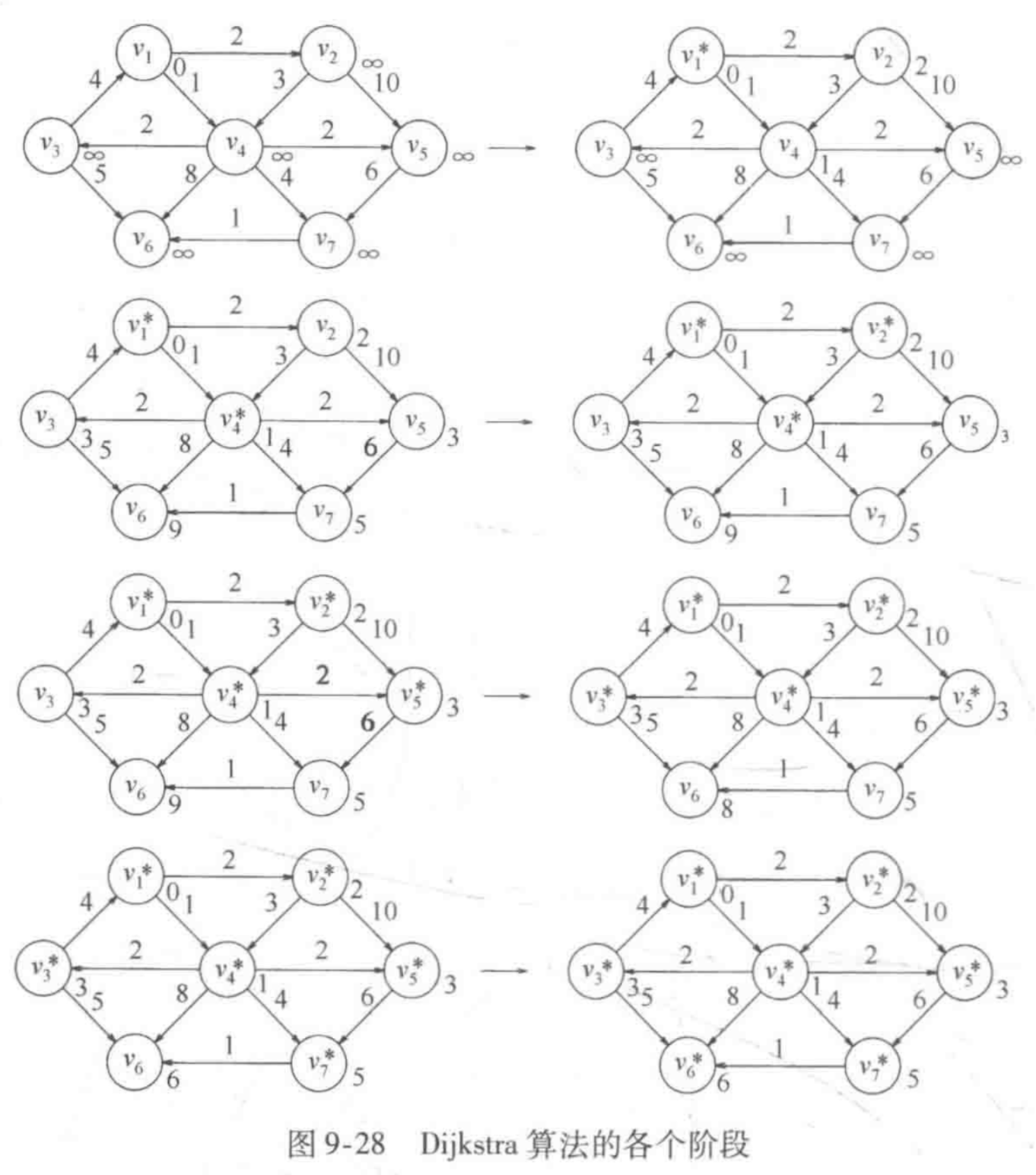
6、迪杰斯特拉算法

dijkstra算法是经典的最短路径算法，用于求解一个节点到其他所有节点的最短路径的问题，它的特点就是：以起始节点为中心，逐层向外面扩展，一致扩展到目标节点为止。也就是以起始节点为树的根节点，然后把距离根节点最近的节点逐个放到树中，知道吧所有的节点（包括目标结点）全部放到树中，这样就找到了起始节点到其他每一个节点的最短路径。它是一种经典的贪婪算法。

dijkstra算法的基本思想如下：

        首先要创建两张表，一个open表，一个close表，用来存储节点的信息。其中open表中保存所有已经生成但是没有被考察过的节点，close表中记录已经访问过的节点。

        （1）搜索图中距离起始节点最近并且没有被考察过的节点，把这个节点放入open表中等待观察

        （2）从open表中找到距离起始节点最近的节点

        （3）找出这个节点的所有子节点，然后把这个节点放入close表

        （4）考察这个节点的所有子节点。首先计算这些子节点到起始节点的距离值，然后把这些子节点全部放到open表中。

        （5）重复第（2）步到第（4）步

1
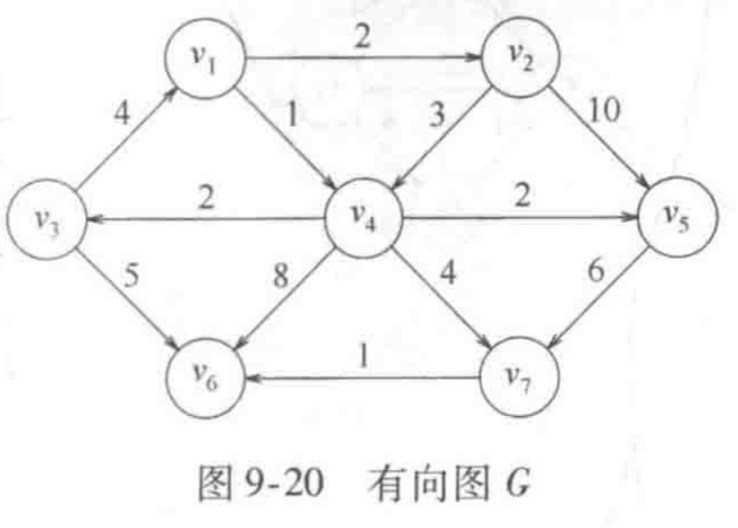
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
1import com.lyf.csdn.graph.graph.Graph;

2import com.lyf.csdn.graph.graph.Point;

3

4import java.util.LinkedList;

5import java.util.List;

6

7/**

8 * 地杰斯特拉算法

9 *

10 * @author yufei.liu

11 */

12public class Dijkstra {

13

14    private Graph graph;

15

16    private Point startPoint;

17

18    private Point endPoint;

19

20    public Dijkstra(Graph graph, Point startPoint, Point endPoint) {

21        this.graph = graph;

22        this.startPoint = startPoint;

23        this.endPoint = endPoint;

24    }

25

26    public void work() {

27        List<Point> open = new LinkedList<>();

28        List<Point> close = new LinkedList<>();

29        int[][] map = graph.getMap();

30        int rowN = map.length;

31        int colN = map[0].length;

32        for (int i = 0; i < rowN; i++) {

33            for (int j = 0; j < colN; j++) {

34                if (map[i][j] == 0) {

35                    close.add(new Point(i, j));

36                }

37            }

38        }

39        close.remove(startPoint);

40        open.add(startPoint);

41

42        Point target = null;

43        while (true) {

44            Point st = null;

45            Point et = null;

46            double distance = Double.MAX_VALUE;

47

48            if (close.isEmpty()) {

49                break;

50            }

51            for (Point openPoint : open) {

52                for (Point closePoint : close) {

53                    double distanceTemp = distance(openPoint, closePoint) + openPoint.getCurrentDistance();

54                    if (distanceTemp < distance) {

55                        st = openPoint;

56                        et = closePoint;

57                        distance = distanceTemp;

58                    }

59                }

60            }

61

62            if (distance >= Integer.MAX_VALUE) {

63                break;

64            }

65            et.setParentPoint(st);

66            et.setCurrentDistance(distance);

67            close.remove(et);

68            open.add(et);

69            if (et.equals(endPoint)) {

70                target = et;

71                break;

72            }

73        }

74        if (target == null) {

75            System.out.println("node is not reachable.");

76        } else {

77            List<Point> result = new LinkedList<>();

78            Point t = target;

79            result.add(t);

80            while (true) {

81                t = t.getParentPoint();

82                if (t == null) {

83                    break;

84                }

85                result.add(t);

86            }

87            graph.printPath(result);

88        }

89

90    }

91

92    /**

93     * 两点之间的距离

94     *

95     * @param start 开始结点

96     * @param end   结束点

97     * @return 距离

98     */

99    private double distance(Point start, Point end) {

100        if (Math.abs(start.getRow() - end.getRow()) > 1 || Math.abs(start.getCol() - end.getCol()) > 1) {

101            return Integer.MAX_VALUE;

102        }

103        if (Math.abs(start.getRow() - end.getRow()) == 0 || Math.abs(start.getCol() - end.getCol()) == 0) {

104            return 1;

105        }

106        return 1.414;

107    }

108

109}

110