最短路径是图论中一个很经典的问题:给定图G(V,E),求一条从起点到终点的路径,使得这条路径上经过的所有边的边权之和最小。
对任意给出的图G(V,E)和起点S、终点T,如何求从S到T的最短路径。解决最短路径问题的常用算法有Dijkstra算法、Bellman-Ford算法、SPEA算法和Floyd算法。
1.Dijkstra算法
Dijkstra算法(读者可以将其读作“迪杰斯特拉算法”)用来解决单源最短路问题,即给定图G和起点s,通过算法得到S到达其他每个顶点的最短距离。Dijkstra的基本思想是对图G(V,B)设置集合S,存放已被访问的顶点,然后每次从集合V-S中选择与起点s的最短距离最小的一个顶点(记为u),访问并加入集合S。之后,令顶点u为中介点,优化起点s与所有从u能到达的顶点v之间的最短距离。这样的操作执行n次(n为顶点个数),直到集合S已包含所有顶点。
单源最短路径:从起点V出发,每个顶点之间的路程尽可能短,即从起点到达其他所有顶点都必须是最短距离。
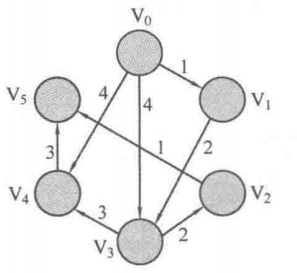
①将地图上所有边都抹去,只有当到达这个顶点后才把从这个顶点出去的边显现(笔者插话:这个操作在实际编写代码时是自然成立、不需要人为控制的,但是在这单独提出来对理解Dijkstra操作的过程很有帮助)。
②在地图中的顶点V(0≤i≤5)上记录从起点V0到达该城市所需要的最短距离。由于在①中所有边都被抹去了,因此在初始状态下除了V0到达V0的距离是0之外,从V到达其他顶点的距离都是无穷大(记为INF)。为了方便叙述,在下文中某几处出现的最短距离都是指从起点V0到达顶点V的最短距离。
下面是行动策略:
①由于要攻占六个顶点,因此将步骤②③执行六次,每次攻占一个顶点(如果是n个顶点,那么就执行n次)。
②每次都从还未攻占的城市中选择当前距离起点V0最近的城市(即地图的顶点上记录的最短距离最小的未到达的顶点,记为Vk(0≤k≤5)。
③到达顶点Vk后,开放地图上从Vk出发的所有边,并査看以Vk为中介点的情况下,能否使从起点V0到达某些还未到达的顶点的最短距离变小。如果能,则将那个最短距离覆盖到对应的城市上(因为开放了从Vk出发的边,因此有了改善某些顶点最短距离的可能,且当前只有Vk能够优化这个最短距离)。
首先,Dijkstra算法解决的是单源最短路问题,即给定图G(V,E)和起点s(起点又称为源点),求从起点s到达其它顶点的最短距离。Dijkstra算法的策略是:设置集合S存放已被访问的顶点(即已到达的顶点),然后执行n次下面的两个步骤(n为顶点个数)。
①每次从集合V-S(即未到达的顶点)中选择与起点s的最短距离最小的一个顶点(记为u),访问并加入集合S(即令其已被访问)。
②之后,令顶点u为中介点,优化起点s与所有从u能到达的顶点v之间的最短距离。
Dijkstra算法的具体实现:由于Dijkstra算法的策略比较偏重于理论化,因此为了方便编写代码,需要想办法来实现策略中两个较为关键的东西,即集合S的实现、起点s到达顶点Vi(0≤i≤n-1)的最短距离的实现。
①集合S可以用一个bool型数组vis[]来实现,即当vis[i]=true时表示顶点Vi已被访问,当vis[i]=false时表示顶点Vi未被访问。
②令int型数组表示起点s到达顶点V的最短距离,初始时除了起点s的的d[s]赋为0,其余顶点都赋为一个很大的数(10^9)来表示INF,即不可达。
接下来看看实现Dijkstra算法的伪代码。其实很短,不难,希望读者能够结合上面好好理解一下这个伪代码,然后再往下看:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2Dijkstra(G,d[],s){
3 初始化
4 for(循环n次){
5 u = 使d[u]最小的还未访问的顶点的标号;
6 记u已被访问;
7 for(从u出发能到达的所有顶点v){
8 if(v未被访问&&以u为中介点使s到顶点v的最短距离d[v]更优){
9 优化d[v];
10 }
11 }
12 }
13}
14
15
由于图可以使用邻接矩阵或者邻接表来实现,因此也就会有两种写法,但是这两种写法都是以上面的伪代码为基础的,区别主要集中在枚举从u出发能到达的顶点v上面:邻接矩阵需要枚举所有顶点来查看v是否可由u到达;邻接表则可以直接得到u能到达的顶点v。在写出具体函数之前,需要先定义MAXV为最大顶点数、INF为一个很大的数字:
2
3
4
2const int INF = 1000000000; //设INF为一个很大的数
3
4
下面来看邻接矩阵和邻接表对Dijkstra算法的具体实现代码。
(1)邻接矩阵版
适用于点数不大(例如V不超过1000)的情况,相对好写。代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2int d[maxv]; //起点到达各点的最短路径长度
3bool vis[MAXV] = {false}; //标记数组,vis[i]==true表示已访问。初始值均为false
4
5void Dijkstra(int s){ //s为起点
6 fill(d,d+MAXV,INF); //fill函数将整个d数组赋值为INF(慎用memset)
7 d[s] = 0; //起点s到达自身的距离为0
8 for(int i=0;i<n;i++){ //循环n次
9 int u=-1,MIN=INF; //u使d[u]最小,MIN存放最小的d[u]
10 for(int j=0;j<n;j++){ //找到未访问的顶点中d[]最小的
11 if(vis[j]==false && d[j]<MIN){
12 u=j;
13 MIN=d[j];
14 }
15 }
16 //找不到小于INF的d[u],说明剩下的顶点和起点s不连通
17 if(u==-1)
18 return;
19 vis[u] = true; //标记u为已访问
20 for(int v=0;v<n;v++){
21 //如果v未能访问&&u能到达v&&以u为中介点可以使d[v]更优
22 if(vis[v]==false && G[u][v] != INF && d[u]+G[u][v] < d[v]){
23 d[v] = d[u]+G[u][v]; //优化d[v]
24 }
25 }
26 }
27}
28
从复杂度来看,主要是外层循环O(V)(V就是顶点个数n)与内层循环(寻找最小的d[u]需要O(V)、枚举v需要O(V))产生的,总复杂度为O(V*(V+V))=O(V^2)。
(2)邻接表版
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2int n; // n为顶点数,图G使用邻接表实现,MAXV为最大顶点数
3int d[maxv]; //起点到达各点的最短路径长度
4bool vis[MAXV] = {false}; //标记数组,vis[i]==true表示已访问。初始值均为false
5
6void Dijkstra(int s){ //s为起点
7 fill(d,d+MAXV,INF); //fill函数将整个d数组赋值为INF(慎用memset)
8 d[s] = 0; //起点s到达自身的距离为0
9 for(int i=0;i<n;i++){ //循环n次
10 int u=-1,MIN=INF; //u使d[u]最小,MIN存放最小的d[u]
11 for(int j=0;j<n;j++){ //找到未访问的顶点中d[]最小的
12 if(vis[j]==false && d[j]<MIN){
13 u=j;
14 MIN=d[j];
15 }
16 }
17 //找不到小于INF的d[u],说明剩下的顶点和起点s不连通
18 if(u==-1)
19 return;
20 vis[u] = true; //标记u为已访问
21 for(int j=0;j<Adj[u].size();j++){
22 int v = Adj[u][j].v; //通过邻接表直接获得u能到达的顶点v
23 if(vis[v]==false && d[u]+Adj[u][j].dis < d[v]){
24 //如果v未能访问&&以u未终结点可以使d[v]更优
25 d[v] = d[u]+G[u][v]; //优化d[v]
26 }
27 }
28 }
29}
30
从复杂度来看,主要是外层循环O(V)与内层循环(寻找最小的d[u]需要O(V)、枚举V需要O(adj[u].size))产生的。又由于对整个程序来说,枚举v的次数总共为O(E),因此总复杂度为O(V^2+E)。
可以注意到,上面的做法都是复杂度O(V)级别的,其中由于必须把每个顶点都标记为已访问,因此外层循环的O(V)时间是无法避免的,但是寻找最小d[u]的过程却可以不必达到O(V)的复杂度,而可以使用堆优化来降低复杂度。最简洁的写法是直接使用STL中的优先队列priority_ queue,这样使用邻接表实现的Dijkstra算法的时间复杂度可以降为O(VlogV+E)。此外,Dijkstra算法只能应对所有边权都是非负数的情况,如果边权出现负数,那么 Dijkstra算法很可能会出错,这时最好使用SPFA算法。
下面以上面的例图为例编写代码,并最终输出从起点V0到达所有顶点(包括V0)的最短距离,程序代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
2#include<algorithm>
3using namespace std;
4const int MAXV = 1000; //最大顶点数
5const int INF = 1000000000; //设INF为一个很大的数
6
7int n,m,s,G[MAXV][MAXV]; //n为顶点数,m为边数,s为起点
8int d[MAXV]; //起点到达各点的最短路径长度
9bool vis[MAXV] = {false}; //标记数组,vis[i]==true表示已访问。初始值均为false
10
11void Dijkstra(int s){ //s为起点
12 fill(d,d+MAXV,INF); //fill函数将整个d数组赋值为INF(慎用memset)
13 d[s] = 0; //起点s到达自身的距离为0
14 for(int i=0;i<n;i++){ //循环n次
15 int u=-1,MIN=INF; //u使d[u]最小,MIN存放最小的d[u]
16 for(int j=0;j<n;j++){ //找到未访问的顶点中d[]最小的
17 if(vis[j]==false && d[j]<MIN){
18 u=j;
19 MIN=d[j];
20 }
21 }
22 //找不到小于INF的d[u],说明剩下的顶点和起点s不连通
23 if(u==-1)
24 return;
25 vis[u] = true; //标记u为已访问
26 for(int v=0;v<n;v++){
27 //如果v未能访问&&u能到达v&&以u未终结点可以使d[v]更优
28 if(vis[v]==false && G[u][v] != INF && d[u]+G[u][v] < d[v]){
29 d[v] = d[u]+G[u][v]; //优化d[v]
30 }
31 }
32 }
33}
34
35int main(){
36 int u,v,w;
37 scanf("%d%d%d",&n,&m,&s); //顶点个数,边数,起点编号
38 fill(G[0],G[0]+MAXV*MAXV,INF); //初始化图G
39 for(int i=0;i<m;i++){
40 scanf("%d%d%d",&u,&v,&w); //输入u,v以及u->v的边权
41 G[u][v] = w;
42 }
43 Dijkstra(s); // Dijkstra算法入口
44 for(int i=0;i<n;i++){
45 printf("%d ",d[i]); //输出所有顶点的最短距离
46 }
47 return 0;
48}
49
输入数据:
2
3
4
5
6
7
8
9
10
20 1 1
30 3 4
40 4 4
51 3 2
62 5 1
73 2 2
83 4 3
94 5 3
10
输出结果:
2
2
有的读者会有疑问,如果题目给出的是无向边(即双同边)而不是有向边,又该如解决呢?这其实很容易,只需要把无向边当成两条指向相反的有向边即可。对邻接矩阵来说,一条u与v之间的无向边在输入时可以分别对G[u][v]和G[v][u]赋以相同的边权;而对邻接表来说,只需要在u的邻接表Adj[u]末尾添加上v,并在v的邻接表Adj[v]末尾添加上u即可。
之前一直在讲最短距离的求解,但是还没有讲到最短路径本身怎么求解。那么接下来学习一下最短路径的求法。在Dijkstra算法的伪代码部分,有这么一段:
2
3
4
2 优化d[v];
3}
4
这个地方提到的条件“以u为中介点可以使起点s到顶点v的最短距离d[v]更优”隐含了这样一层意思:使d[v]变得更小的方案是让u作为从s到v最短路径上v的前一个结点(即s→…→u→v)。这就给我们一个启发:不妨把这个信息记录下来。于是可以设置数组pre[]令pre[v]表示从起点s到顶点v的最短路径上v的前一个顶点(即前驱结点)的编号。这样当伪代码中的条件成立时,就可以将u赋给pre[v],最终就能把最短路径上每一个顶点的前驱结点记录下来。而在伪代码部分只需要在if内增加一行:
2
3
4
5
2 优化d[v];
3 令v的前驱为u;
4}
5
具体实现中,以邻接矩阵为例:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2int d[maxv]; //起点到达各点的最短路径长度
3int pre[MAXV]; //pre[v]表示从起点到顶点v的最短路径v的前一个顶点
4bool vis[MAXV] = {false}; //标记数组,vis[i]==true表示已访问。初始值均为false
5
6void Dijkstra(int s){ //s为起点
7 fill(d,d+MAXV,INF); //fill函数将整个d数组赋值为INF(慎用memset)
8 for(int i=0;i<n;i++)
9 pre[i] = i; //初始状态设每一个点的前驱为自身
10 d[s] = 0; //起点s到达自身的距离为0
11 for(int i=0;i<n;i++){ //循环n次
12 int u=-1,MIN=INF; //u使d[u]最小,MIN存放最小的d[u]
13 for(int j=0;j<n;j++){ //找到未访问的顶点中d[]最小的
14 if(vis[j]==false && d[j]<MIN){
15 u=j;
16 MIN=d[j];
17 }
18 }
19 //找不到小于INF的d[u],说明剩下的顶点和起点s不连通
20 if(u==-1)
21 return;
22 vis[u] = true; //标记u为已访问
23 for(int v=0;v<n;v++){
24 //如果v未能访问&&u能到达v&&以u未终结点可以使d[v]更优
25 if(vis[v]==false && G[u][v] != INF && d[u]+G[u][v] < d[v]){
26 d[v] = d[u]+G[u][v]; //优化d[v]
27 pre[v] = u; //记录v的前驱顶点是u
28 }
29 }
30 }
31}
32
新增的只有3、8~9、27行。
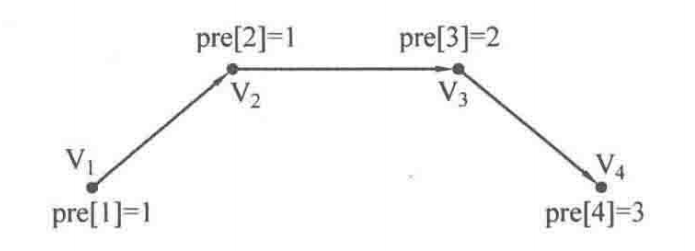
到这一步,只是求出了最短路径上每个点的前驱,那么如何求整条路径呢?以下图这个很简单的路径来说明。从算法中已经可以得到了每个顶点的前驱:
2
3
4
5
2pre[3] = 2;
3pre[2] = 1;
4pre[3] = 1;
5
那么,当想要知道从起点V1到达V4的最短路径,就需要先从pre[4]得到V4的前驱顶点是V3,然后从pre[3]得到V3的前驱顶点是V2,再从pre[2]得到V2的前驱顶点是V1。
这听起来有点像递归?没错,就是用递归不断利用pre[]的信息寻找前驱,直至到达起点V1后从递归深处开始输出。
这个递归写起来很简洁,读者可以好好体会一下:
2
3
4
5
6
7
8
9
2 if(v ==s){ //如果当前以及到达起点s,则输出起点并返回
3 printf("%d\n",s);
4 return;
5 }
6 DFS(s,pre[v]); //递归访问v的前驱顶点pre[v]
7 printf("%d\n",v); //从最深处return回来之后,输出每一层的顶点号
8}
9
至此,Dijkstra算法的基本用法大家都应该已经掌握。但是题目肯定不会考得这么“裸”,更多时候会出现这样一种情况,即从起点到终点的最短距离最小的路径不止一条。例如上面的例子中如果把V0→V3的距离改为3,那么从V0→V3就会有两条最短路径,即V0→V1→V3与V0→V3,它们都可以达到最短路径3。
于是,碰到这种有两条及以上可以达到最短距离的路径,题目就会给出一个第二标尺(第一标尺是距离),要求在所有最短路径中选择第二标尺最优的一条路径。而第二标尺常见的是以下三种出题方法或其组合:
①给每条边再增加一个边权(比如说花费),然后要求在最短路径有多条时要求路径上的花费之和最小(如果边权是其他含义,也可以是最大)。
②给每个点增加一个点权(例如每个顶点能得到的权重),然后在最短路径有多条时要求路径上的点权之和最大(如果点权是其他含义的话也可以是最小)。
③直接问有多少条最短路径。
对这三种出题方法,都只需要增加一个数组来存放新增的边权或点权或最短路径条数,然后在Dijkstra算法中修改优化d的那个步骤即可,其他部分不需要改动。下面对这三种出题方法对代码的修改给出解释:
①新增边权。以新增的边权代表花费为例,用 cost[u][v]表示u→v的花费(由题目输入),并增加一个数组c[],令从起点s到达顶点u的最少花费为c[u],初始化时只有c[]为0、其余c[u]均为INF。这样就可以在d[u]+G[u][v]<d[v](即可以使s到v的最短距离更优)时更新d[v]和c[v],而当d[u]+G[u][v]=d[v](即最短距离相同)且c[u]+cost[u][v]<c[v](即可以使s到v的最少花费更优)时更新c[v]。代码如下:
2
3
4
5
6
7
8
9
10
11
12
2 // 如果v未访问&&u能到达v
3 if(vis[v]==false G[u][v] != INF){
4 if(d[u] + G[u][v] < d[v]){ //以u未终结点可以是d[v]更优
5 d[v] = d[u] + G[u][v];
6 c[v] = c[u] + cost[u][v];
7 } else if(d[u] + G[u][v] ==d[v] && c[u] + cost[u][v] < c[v]){
8 c[v] = c[u] + cost[u][v]; //最短距离相同时看能否使c[v]更优
9 }
10 }
11}
12
②新增点权。以新增的点权代表顶点中能得到的权重为例,用 weight[u]表示城市u中的物资数目(由题目输入),并增加一个数组w[],令从起点s到达顶点u可以收集到的最大物资为w[u],初始化时只有w[s]为 weight[s]、其余w[u]均为0。这样就可以在d[u]+G[u][v]<d[v](即可以使s到v的最短距离dv更优)时更新d[v]和c[v],而当d[u]+G[u][v]=d[v](即最短距离相同)且w[u]+weight[v]>w[v](即可以使s到v的最大物资数目更优)时更新w[v]。代码如下:
2
3
4
5
6
7
8
9
10
11
12
13
2 // 如果v未访问&&u能到达v
3 if(vis[v]==false G[u][v] != INF){
4 if(d[u] + G[u][v] < d[v]){ //以u未终结点可以是d[v]更优
5 d[v] = d[u] + G[u][v];
6 w[v] = w[u] + weight[v];
7 } else if(d[u] + G[u][v] ==d[v] && w[u] + weight[v] > w[v]){
8 w[v] = w[u] + weight[v]; //最短距离相同时看能否使w[v]更优
9 }
10 }
11}
12
13
③)求最短路径条数。只需要增加一个数组num[],令从起点s到达顶点u的最短路径条数为num[u],初始化时只有num[u]为1、其余num[u]均为0。这样就可以在d[u]+G[u][v]<d[v](即可以使s到v的最短距离d[v]更优)时更新d[v],并让num[v]继承num[u],而当d[u]+G[u][v]=d[v](即最短距离相同)时将 num[u]加到num[v]上。代码如下:
2
3
4
5
6
7
8
9
10
11
12
2 // 如果v未访问&&u能到达v
3 if(vis[v]==false G[u][v] != INF){
4 if(d[u] + G[u][v] < d[v]){ //以u未终结点可以是d[v]更优
5 d[v] = d[u] + G[u][v];
6 num[v] = num[u];
7 } else if(d[u] + G[u][v] ==d[v]){
8 num[v] += num[u]; //最短距离相同时累加num
9 }
10 }
11}
12
以上就是Dikjstra的全部内容。
